– OVER DE GRENZEN VAN DE REDE –
1. Vooraf – 2. Hoe wij denken – 3. Waanzin: een zeer korte inleiding – 4. De omgekeerde wereld –
5. Het narrenschip – 6. Archimedes’ waanzinnige meesterbrein –
7. De wanen van wijlen dris. Piet Vroon, psycholoog – 8. Het waanland Xamara – 9. Droomtijd
Archimedes’ waanzinnige meesterbrein
Op een mooie, zonnige dag in de derde eeuw voor Christus rende er een naakte, kletsnatte man over de drukke agora van de Siciliaanse havenstad Syracuse, destijds een zelfstandige stadstaat in het Griekse rijk.

Toen de mensen die hem meenden te kennen als een wijs en bedachtzaam man hem verbaasd staande hielden en vroegen: ‘Archimedes, wat is er aan de hand?’, riep hij: ‘Eureka’ (ik heb het gevonden). Zo ongeveer gaat het verhaal zoals het tweehonderd jaar later voor het eerst is opgetekend door Marcus Vitruvius Pollio, Romeins architect, artillerist in het leger van Julius Caesar en auteur van het tiendelige De Architectura (Over de architectuur). Een eeuw daarna is het nog eens naverteld door de geschiedschrijver Plutarchus in diens Vitae Parallelae (Vergelijkbare levens), maar het is zeer de vraag of dat voorval ook werkelijk zo heeft plaatsgevonden. Naarmate de tijd verstrijkt blijkt een verslag zich steeds verder van de ware gebeurtenissen te verwijderen, en degenen die het zoveel jaren later opschrijven doen vaak hun best hun helden wat beter uit de verf te laten komen door ze heroïscher voor te stellen dan ze in werkelijkheid waren, en dat zal in geval van Archimedes niet anders zijn geweest. Gelukkig voor ons maakt dat voor de verdere geschiedenis weinig uit, want hebben mooie en leerzame verhalen niet evenveel bestaansrecht als beschrijvingen van ware gebeurtenissen?
Over het sterfjaar van Archimedes bestaat wel enige zekerheid, omdat hij tijdens de Tweede Punische oorlog tussen de grootmachten Rome en Carthago bij de inname van zijn geboortestad Syracuse in 212 v.Chr. door een soldaat van het Romeinse leger werd omgebracht, een gebeurtenis die meermalen door antieke geschiedschrijvers is opgetekend. En omdat de twaalfde-eeuwse Byzantijnse historicus Johannes Tzetzes – overigens zonder verder bewijs − ergens vermeldt dat hij toen de gezegende leeftijd van 75 jaar had bereikt, zal hij wel omstreeks 287 v.Chr. geboren zijn. Wat we weer niet zeker weten is of hij wel Archimedes heette, want die naam betekent zoiets als ‘meesterbrein’, wat net zo goed een erenaam van zijn bewonderaars als zijn echte naam kan zijn geweest, maar dat hij een meesterbrein hád is boven elke twijfel verheven. Marcus Tullius Cicero hield hem voor een groter genie dan voor een mens mogelijk werd geacht, ook Galileo Galilei noemde hem ‘bovenmenselijk’ en Voltaire vond dat er in Archimedes’ hoofd meer verbeeldingskracht zat dan in dat van Homerus.
Archimedes rende naakt en nat over het marktplein omdat hij tijdens het baden had nagedacht over een moeilijk probleem en plotseling werd getroffen door een geniale inval. Opgetogen was hij uit het bad gesprongen en zonder aan zijn kleren te denken naakt naar buiten gerend. Hoewel, naakt? In de antieke Griekse wereld werd ‘zonder overkleed’ ook al naakt gevonden, dus misschien viel het allemaal wel mee. Erg vaak zat Archimedes overigens niet in het bad, want volgens Plutarchus was hij zo waanzinnig bezeten door de muze van de wiskunde en vertoefde hij voortdurend in zulke hoge sferen dat hij vergat te eten en niet aan zijn lichamelijke hygiëne dacht. Pas als de kwalijke geur die hij verspreidde voor zijn omgeving niet meer te verdragen was, werd hij door zijn vrienden met enige dwang in bad gestopt, gewassen en gezalfd, terwijl hij zelf onverstoorbaar doorging met zijn vingers figuren te tekenen in het zand op de vloer, in het as van het vuur en in de olie op zijn lichaam. Diezelfde bezetenheid door de muze van de wiskunde betekende ook het eind van zijn leven, omdat – hoewel hij de leiding van de verdediging van de stad op zich had genomen − de inname en de plundering van Syracuse na jaren belegering door het Romeinse leger ongemerkt aan hem voorbij was gegaan. Toen hij in gedachten verzonken over een paar in het zand op de vloer getekende figuren gebogen zat kwam er een soldaat binnen die waarschijnlijk alleen uit was op de roof van kostbaarheden en niet wist wie hij voor zich had. ‘Bederf mijn cirkels niet’ of ‘blijf uit de buurt van mijn tekening’ schijnt Archimedes verstoord gezegd te hebben, waarna de getergde soldaat die vervelende oude man aan zijn zwaard reeg.

Terwijl de Romeinse generaal Marcus Claudius Marcellus, die Archimedes mateloos bewonderde en graag over zijn kennis van oorlogsmachines wilde beschikken, nog uitdrukkelijk de opdracht had gegeven zijn leven te sparen. Tenslotte had de generaal ondanks zijn enorme vloot en landleger door Archimedes’ inventiviteit de ene na de andere nederlaag moeten incasseren en de stad niet na strijd maar weinig eervol pas na twee jaar uithongeren kunnen innemen. Het kan ook zijn dat de soldaat hem wel herkende en de opdracht had hem naar Marcellus te brengen, maar dat Archimedes toen zei daar geen tijd voor te hebben omdat hij eerst het probleem waarmee hij bezig was moest oplossen, met hetzelfde noodlottige gevolg. Er is ook nog een derde versie van dit verhaal, die inhoudt dat Archimedes met zijn wetenschappelijke instrumenten onder zijn arm gedwee met de soldaat wilde meegaan en deze, in de veronderstelling dat het om kostbaarheden ging, de bezitter doodde en beroofde.
Archimedes was in elk geval dood, en ontdaan over de misplaatste moord gaf Marcellus opdracht tot het organiseren van een grootse begrafenis in de necropolis van Syracuse vlak buiten de stad. Op het graf liet hij een monument oprichten bestaande uit een bol die wordt omsloten door een cilinder van dezelfde hoogte en diameter. Dat was volgens de uitdrukkelijke wens van Archimedes zelf, omdat hij het bewijs dat zowel het oppervlak als de inhoud van de bol tweederde deel van die van de cilinder inclusief de beide cirkelvormige grensvlakken uitmaakt, tot een van zijn beste wiskundige prestaties rekende.
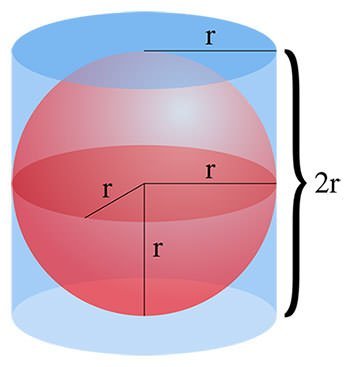
De inwoners van Syracuse waren zich minder bewust van Archimedes’ beroemdheid, want toen Cicero in 75 v.Chr. Sicilië als Romeinse administrateur bezocht, ging hij op zoek naar de plaats waar de grootste wiskundige uit de Oudheid 137 jaar eerder begraven moest zijn, en merkte toen tot zijn verbazing dat geen van de notabelen bekend was met hun tijdens zijn leven zo gevierde landgenoot en ook niet wisten waar zijn graf lag. Uiteindelijk lukte het Cicero zelf op een verwaarloosde begraafplaats het door struikgewas overwoekerde graf te vinden, met daarop inderdaad de in een cilinder gevatte bol. Maar ook die ontdekking is weer verloren gegaan, want ondanks een enkele dubieuze claim van een lokale, op winst beluste hotelhouder weet tegenwoordig niemand meer waar Archimedes precies begraven ligt.
Afgezien van de korte periode in zijn jeugd die hij op uitnodiging van de Egyptische koning Ptolemeus II aan het Museon in Alexandrië studeerde, waar hij zijn levenslange vriend en collega Conon van Samos leerde kennen en hij eventueel Apollonius van Rhodos zou hebben kunnen ontmoeten, heeft Archimedes zijn hele bestaan in Syracuse doorgebracht. Onder welke sociale en economische omstandigheden hij daar leefde is ook al een punt van speculatie en discussie. Cicero vermeldt dat hij ‘een bescheiden, kleine man’ was, maar dat kan betrekking hebben op zowel zijn postuur als zijn karakter of sociale status. Plutarchus vermoedt dat hij een goede vriend en mogelijk zelfs een verre verwant was van koning Hiero II van Syracuse. En Plutarchus’ tijdgenoot de dichter Sillius Italicus schreef in zijn epische kroniek van de Tweede Punische Oorlog dat Archimedes alleen voldoening vond in de studie van de wiskunde, over weinig financiële middelen beschikte, maar mogelijke enige vorm van patronage van Hiero ontving, maar dat is allemaal pas veel later opgetekend. Een vriend van Archimedes met de naam Heracleides heeft weliswaar een biografie over hem geschreven, maar die is verloren gegaan, zodat we over de details van zijn persoonlijke leven wel altijd in het ongewisse zullen blijven. We weten niet eens of hij getrouwd was en kinderen had. Van Archimedes zelf kennen we alleen de mededeling dat zijn vader Phidias heette en had nagedacht over de omvang van het universum, dus mogelijk astronoom of astroloog moet zijn geweest. Wel is er zeventig jaar na zijn dood een verslag van het beleg van Syracuse geschreven door de Griekse historicus Polybius in zijn Historiën, waarin weinig over de persoon Archimedes is te vinden, maar waarin wel zijn cruciale rol bij de verdediging van de stad wordt belicht, en dat later door Titus Livius en Plutarchus als bron is gebruikt. Pas in 530 n.Chr. publiceerde de Byzantijnse wiskundige en architect Isidorus van Milete een min of meer volledige overzicht van wat men toen over Archimedes meende te weten, terwijl de wiskundige Eutocius van Ascalon al eerder in diezelfde eeuw voor een breder publiek toegankelijke commentaren op zijn werk had geschreven.
Waar Archimedes volgens het verhaal in zijn badkuip over nadacht was een probleem dat Hiero hem had voorgelegd. De koning had de goudsmid in zijn dienst een bepaald gewicht aan zuiver goud bezorgd en hem gevraagd daar een kunstig gevlochten kroon van te maken om volgens een gelofte die hij had gedaan een godenbeeld in de tempel mee te tooien. Maar de koning was niet helemaal gerust over de betrouwbaarheid van de smid en toen de kroon klaar was gaf hij Archimedes de opdracht om zonder het heilige sieraad te beschadigen uit te zoeken of het wel zuivere koffie was en de smid er geen hoeveelheid goedkoper zilver doorheen had gemengd om het overeenkomstige gewicht aan goud in zijn eigen zak te kunnen steken. Toen Archimedes daarover peinzend door zijn vrienden in het warme badwater werd neergelaten vielen hem twee dingen op. Ten eerste zag hij dat het niveau van het water in de badkuip steeg, wat hem niet verbaasde omdat er door het volume van zijn lichaam een gelijke hoeveelheid water werd verplaatst, maar hij voelde zich ook lichter worden en wat hij plotseling inzag was dat de vermindering van zijn eigen gewicht gelijk moest zijn aan dat van de hoeveelheid verplaatst water. Het totale gewicht van de kuip met water plus Archimedes moest immers gelijk blijven, hoever hij zich ook onderdompelde. En omdat Archimedes ook nog wist dat een zilveren dobbelsteen minder weegt dan een zelfde dobbelsteen van goud, vond hij daarin de oplossing van zijn probleem. Een met zilver vervalste kroon, hoe ingewikkeld van vorm ook en van hetzelfde gewicht als een kroon van zuiver goud, zou een groter volume moeten innemen en onder water, door de grotere hoeveelheid verplaatste vloeistof, minder moeten wegen: ‘Eureka!’ Toen Archimedes goed en wel van zijn ren over het marktplein in zijn werkruimte was bekomen, liet hij een blok zuiver goud van hetzelfde gewicht als de kroon in een precies tot de rand met water gevulde badkuip zakken, zodat er water over de rand vloeide, haalde het goud er voorzichtig uit waardoor het niveau van het water iets daalde, en liet vervolgens de kroon in het water zakken, waarna hij eenvoudig kon vaststellen dat er nog wat water over de rand liep en de kroon een groter volume moest hebben dan het goudblok.
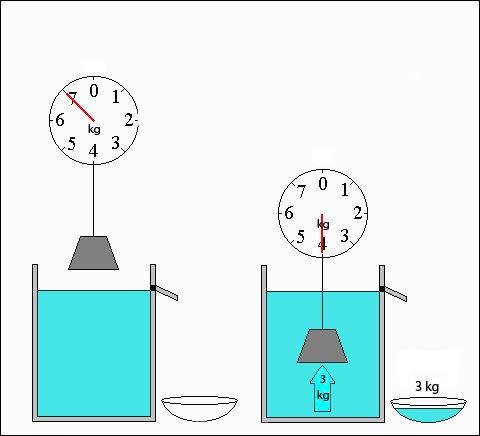
Geconfronteerd met dit bewijs bekende de goudsmid schuld, werd zwaar gestraft voor de misdaad die hij de tempelgod en de koning had aangedaan, en Archimedes’ faam was voorgoed gevestigd. Of dat ook werkelijk zo is gebeurd wordt inmiddels alom betwijfeld omdat daarvoor een veel grotere nauwkeurigheid voor het experiment vereist is dan Archimedes waarschijnlijk kon opbrengen, en er zijn, onder anderen door Galileï, ook wel alternatieve experimenten bedacht die hij wel zou hebben kunnen uitvoeren, maar nogmaals, mooie en leerzame verhalen hebben evenzeer bestaansrecht als zogenaamd correcte beschrijvingen van werkelijke gebeurtenissen. Het echte belang van Archimedes’ ontdekking ligt dan ook niet in dit specifieke geval van de kroon, maar dat hij daarmee het algemene principe formuleerde dat de opwaartse druk die geheel of gedeeltelijk ondergedompelde voorwerpen ondervinden gelijk is aan het gewicht van de hoeveelheid verplaatste vloeistof, wat bepalend is voor bijvoorbeeld het drijfvermogen en de stabiliteit van schepen.
Ondanks de praktische toepassingen die zijn denkwerk bleek te hebben was Archimedes als ware platonist in de eerst plaats geïnteresseerd in de zuivere wiskunde. Plutarchus vermeldt in zijn Vitae Parallelae dat hij
al het construeren van werktuigen en andere kunsten die nut of winst afwerpen als onedel en minderwaardig verwierp, en zijn hele eerzucht plaatste in die speculaties waarvan de schoonheid en de diepzinnigheid buiten contact met de gewone noodzaken van het leven blijven.
Zijn werk op het gebied van de zuivere wiskunde is dan ook zonder meer geniaal te noemen, vergelijkbaar met dat van Isaac Newton, Gottfried Leibniz en Carl Gauss zoveel eeuwen later. Hij leidde de wiskundige eigenschappen af van parabolen, spiralen en veelvlakken, ontwikkelde nieuwe manieren om wortels en booglengtes te bepalen en de inhoud van bollen, cilinders en kegels te berekenen. Zijn belangrijkste prestatie, die aan de basis ligt van vele andere, is evenwel zijn ingenieuze methode om de omtrek van een cirkel te bepalen en daarmee de waarde van het irrationele getal π, dat is gedefinieerd als de verhouding tussen de omtrek en de diameter (of twee maal de straal) van een cirkel: π = cirkelomtrek/2r. Daaruit kon hij afleiden dat ook de oppervlakte van een cirkel in π kan worden uitgedrukt: π = cirkeloppervlak/r2. Hij deed dat door een cirkel te tekenen met daarbinnen een zeshoek met de hoekpunten op de cirkelomtrek en daaromheen een grotere zeshoek met de zijden als raaklijnen aan de omtrek van de cirkel. De oppervlakken van de zeshoeken, die heel in de verte op een cirkel lijken, rekende hij uit door ze in driehoeken te verdelen en de stelling van zijn belangrijkste voorganger Pythagoras toe te passen.

Omdat het oppervlak van de cirkel tussen dat van de twee zeshoeken in moet liggen had Archimedes met deze wiskundige truc een ruwe onder- en bovengrens van π bepaald, en door vervolgens het aantal zijden van de veelhoek in en om de cirkel te verdubbelen en zo steeds meer op een cirkel te laten lijken, kreeg hij ook een steeds betere benadering. In het limietgeval van oneindig veel verdubbelingen zouden de veelhoeken de cirkel niet meer benaderen, maar er allebei precies mee samenvallen. Na vier maal verdubbelen tot een 96-hoek vond Archimedes dat de waarde van π in onze decimale notatie tussen 3,1429 en 3,1408 moet liggen, wat dicht in de buurt ligt van de werkelijke waarde 3,1416. Dat hij vervolgens de inhoud van een bol, een cilinder en een kegel kon bepalen door een cirkel om de middellijn, een rechthoek om zijn assen en een vierkant op zijn punt om een diagonaal te draaien vereist dan geen aan waanzin grenzende genialiteit meer. Ook lukte het hem het oppervlak uit te rekenen van het gebied dat door een rechte lijn van een parabool wordt afgesneden. Het speciale belang hiervan is dat hij de parabool beschouwde als de ideale vorm van een scheepsromp, en hij op die manier aan de stabiliteit en het drijfvermogen van schepen kon rekenen. Het meest verbazend echter is dat Archimedes met deze benaderingsmethoden het principe heeft blootgelegd van de differentiaal- en integraalrekening, of infinitisimaalrekening, die pas tweeduizend jaar later door Newton en Leibniz zou worden herontdekt en verder worden uitgewerkt tot een van de steunpilaren van de moderne wiskunde.
De grootsheid van Archimedes’ prestatie wordt des te merkwaardiger als in aanmerking wordt genomen dat hij niet beschikte over de symboliek, de vergelijkingen en de diagrammen waarvan de moderne wiskunde gebruik maakt. De antieke Grieken beschouwden getallen niet als abstracte grootheden, maar als taalelementen die onlosmakelijk aan een verzameling concrete voorwerpen waren verbonden. Het getal drie had geen zelfstandige, abstracte betekenis en bestond alleen maar voor zover het betrekking had op drie vrouwen, runderen, kookpotten of wat voor andere voorwerpen dan ook, en het getal nul bestond niet omdat een verzameling van nul voorwerpen als absurditeit werd gezien, evenals het negatieve getal dat aan een schuld van drie runderen zou kunnen worden verbonden. Daarom waren Archimedes en zijn wiskundige tijdgenoten gedwongen hun analyses in wijdlopig, breedsprakig en ingewikkeld proza uit te schrijven, wat een van de redenen voor het latere verval van de Griekse wiskunde is geweest. In het maken van meetkundige figuren waren de Grieken meesters, maar aan enige vorm van algebra zijn ze niet toegekomen, mogelijk omdat een adequaat systeem van symbolen daarvoor ontbrak. De letters van het alfabet die wij daar tegenwoordig voor gebruiken waren in de Oudheid al toegewezen aan de getallen en de muzieknoten, zodat er voor de algebraïsche onbekenden geen apart notatiesysteem meer voorhanden was. Pas in de derde eeuw n.Chr. was het de Alexandrijnse wiskundige Diophantus die als eerste een symbool gebruikte om een onbekende in een algebraïsche vergelijking aan te duiden.
Archimedes was in het bijzonder geïnteresseerd in grote getallen en ontwikkelde ook een systeem om die in myriaden (10.000-tallen) uit te drukken. Dat hij zich zelfs een voorstelling probeerde te maken van oneindigheid blijk uit zijn stelling dat ‘iedere grootheid die vaak genoeg bij zichzelf wordt opgeteld iedere gegeven grootheid zal overtreffen’. Om ook zijn vader te overtreffen en om indruk te maken op zijn Koninklijke beschermheer Hiero, zocht Archimedes naar een groter en indrukwekkender model voor het universum dan het in zijn tijd algemeen aanvaarde geocentrische, door Aristoteles gepropageerde systeem met zijn hemelsferen die concentrisch rond de onbeweeglijke aarde wentelen, en qua omvang makkelijk binnen ons zonnestelsel zou passen. Daarom koos hij voor het heliocentrische systeem van zijn oudere tijdgenoot en collega Aristarchus van Samos, dat pas 1800 jaar later door Nicolaus Copernicus zou worden herontdekt. De grotere autoriteit van Aristoteles die in de hoofdstad Athene verbleef, was er mede de oorzaak van dat diens ideeën de voorkeur kregen boven die van Archimedes die immers in het buitengewest Syracuse woonde, wat een vertraging van bijna twee millennia in de ontwikkeling van de astronomie heeft betekend.
Als uitgangspunt voor zijn berekening van de grootte van het universum nam Archimedes de in die tijd vigerende analogie tussen de microkosmos en de macrokosmos, wat inhield dat hij vanzelfsprekend aannam dat de afstand van de aarde tot de sterren (stel x) zich verhoudt tot de straal van de aardbaan (stel a) als de straal van de aardbaan tot de straal van de aarde (stel b). En omdat hij een idee meende te hebben over de stralen van de aarde en de aardbaan kon hij de straal en de inhoud van het universum bepalen: Inhoud = 4/3 πx3 met x = a2/b, maar dan zoals gezegd in proza uitgelegd en zonder het gebruik van wiskundige symbolen. Op uitdaging van Gelo II, de zoon van Hiero, kon hij nu ook uitrekenen hoeveel zandkorrels daar in zouden passen. Hij schreef:
Sommigen, Koning Gelo, denken dat het aantal zandkorrels in het universum niet te tellen is, en met die zandkorrels bedoel ik niet alleen het zand in de buurt van Syracuse, zelfs niet op heel Sicilië, maar ook wat er verder op de hele wereld is te vinden in alle bewoonde en onbewoonde streken.
In zijn verhandeling De zandrekenaar daarover kwam Archimedes met behulp van zijn myriadensysteem in hedendaagse notatie tot het aantal van 8×1063 zandkorrels, wat wil zeggen een 8 met 63 nullen, wat wel heel veel is maar niet ontelbaar. Misschien klopt dat getal niet helemaal, want voor het bepalen van de afmeting van een zandkorrel gebruikte hij geen zand, maar papaverzaadjes die hij ongeveer even groot veronderstelde. Er is niets over bekend, maar het is goed mogelijk dat Archimedes naast de gebruikelijke wijn de papaverzaadjes na zijn metingen niet weggooide maar gebruikte voor het stimuleren van zijn geest.
Zijn kennis van het universum gebruikte Archimedes vervolgens voor het bouwen van een planetarium, waarop hij bijzonder gesteld moet zijn geweest omdat het volgens de wiskundige Pappus van Alexandrië het enige technische werkstuk is waarover hij zelf heeft geschreven. Cicero beweert het instrument ook werkelijk te hebben gezien en beschrijft het als een ingewikkeld bronzen mechanisme met bollen die de zon, de maan en de vijf toen bekende planeten voorstellen en die door een raderwerk van tandwielen kunnen worden aangedreven met de relatieve snelheden waarmee ze gezien vanaf de centrale aarde langs het firmament bewegen. Ook de schijngestalten van de maan en de maans- en zonsverduisteringen zouden er mee aangegeven kunnen worden, en dat alles omsloten door een met sterren bezaaide bol die het hele universum moest voorstellen. Vandaar dat Cicero Archimedes voor een waanzinniger genie kon houden dan voor een mens mogelijk is. Er is dan ook lang gedacht dat de kennis in die tijd niet toereikend kan zijn geweest om iets dergelijks te maken, totdat er in 1900 in een scheepswrak uit de eerste eeuw v.Chr. bij het Griekse eiland Antikythera een door het zoute water van de Middellandse Zee ernstig aangetast metalen mechanisme werd gevonden dat gecompliceerd genoeg is om als aandrijving voor een planetarium te kunnen dienen.

In een fictieve dialoog vermeldt Cicero ook nog dat generaal Marcellus een dergelijk model uit Syracuse als oorlogsbuit voor zichzelf had meegenomen. Opvallend genoeg was het dus geen heliocentrisch model van het universum, wat gezien Archimedes ideeën toch eerder in de lijn der verwachtingen zou liggen.
Als ander voorbeeld van zijn belangstelling voor grote getallen becijferde Archimedes uit hoeveel stuks vee de kudde van de zonnegod Helios, die voorkomt in boek 12 van Homerus’ Odyssee, moet hebben bestaan. De enorme kudde was aan het grazen op de weidegronden van Sicilië toen Odysseus’ hongerige bemanning daar aan land ging, er een paar stuks van slachtte en daarmee de toorn en de wraak van de goden over zich afriep met dramatische gevolgen. Archimedes goot het probleem in een wiskundige vorm door het aantal koeien en stieren van verschillende kleuren in een serie vergelijkingen met evenzoveel onbekenden uit te drukken. Het is niet waarschijnlijk dat hij het probleem ook zelf kon oplossen, maar de Duitse wiskundige August Amthor kwam in 1880 tot de slotsom dat de kudde te groot zou zijn om in een bol met een diameter van tienduizend lichtjaar te passen, waar Sicilië dus lang niet groot genoeg voor is. Pas na de ontwikkeling van de computer lukte het in 1965 om het getal, 7,76×10206544 (naar boven afgerond een 8 met 206544 nullen), met behulp van 1620 gekoppelde IBM-computers en acht uur rekentijd te bepalen, een veel te grote kudde vee om in het ons hele bekende universum te kunnen onderbrengen.
Afkomstig van Archimedes’ meer speelse geest is de zogenaamde stomachionpuzzel, een soort tangramspel bestaande uit een vierkant van ivoor dat is verdeeld in totaal veertien drie-, vier- en vijfhoeken, die op 17.152 verschillende manieren een even groot vierkant kunnen vormen, maar ook in allerlei andere figuren kunnen worden gelegd: een olifant, een beer, een vliegende gans, een gewapende gladiator, een gehurkte jager, een blaffende hond, een toren, een drinkkan en nog heel veel meer.

Ondanks zijn voorkeur voor het zuiver wiskundige denkwerk heeft Archimedes ook vele belangrijke bijdragen geleverd aan de meer praktijkgerichte natuurkunde en de mechanica. Zijn concept van het zwaartepunt, dat nu tot de basiskennis van natuurkundestudenten behoort, vormde de eerste vereenvoudigende abstractie van stoffelijke voorwerpen met als doel de natuur via benaderende modellen beter te kunnen bestuderen, beschrijven en begrijpen. Hij zocht naar de eenheid van wis- en natuurkunde die nog steeds het uitgangspunt vormt van het moderne natuurwetenschappelijke onderzoek. Hij heeft een verhandeling over de eigenschappen van spiegels geschreven – in ieder geval maakte de tweede-eeuwse Latijnse schrijver Lucius Apuleius Madauresis, auteur van de beroemde roman De gouden ezel, daar melding van, maar zonder verwijzing naar mogelijk gebruik van spiegels als wapen − en zijn werk over de opwaartse druk kende in de antieke wereld zijn weerga niet.
Als er op werd aangedrongen was Archimedes ook een meester in het doen van technische en praktisch toepasbare uitvindingen. De met de hand bediende irrigatiepomp, bekend als de schroef van Archimedes, door hem bedacht, of in ieder geval door hem overgenomen toen hij in Alexandrië verbleef, wordt ook tegenwoordig nog gebruikt.

Hij ontwierp zowel een door stoom aangedreven kanon als een op perslucht werkend orgel, en was ook zeer vaardig in het gebruik van hefbomen en katrollen, waarover hij tegen koning Hiero II heeft gezegd: ‘Geef me een hefboom die lang genoeg is en een vaste plaats om op te staan en ik zal de aarde bewegen,’ waarmee hij de fictieve plaats in het universum bedoelde die we tegenwoordig ‘Archimedisch punt’ noemen en volgens onze huidige inzichten niet bestaat. Wat hij wilde zeggen was dat hij met behulp van een geschikte hefboom een kleine kracht zozeer kon vergroten dat hij daarmee in zijn eentje weliswaar niet de hele aarde, maar wel een enorm schip kon verplaatsen.

Als er werkelijk een gebeurtenis heeft plaatsgevonden die Archimedes’ vaardigheden met katrollen en hefbomen bewees dan was het de tewaterlating van de Syracusia, het grootste schip uit de Oudheid, een combinatie van oorlogsbodem en passagiersschip, door hem ontworpen en gebouwd in opdracht van koning Hiero II, een soort wonderschip als de Argo, als cadeau voor de Egyptische heerser Ptolemaeus II. Zoals onder anderen de tweede-eeuwse Alexandrijnse taalkundige Athenaeus van Naucratis het opschreef was de Syracusia 110 meter lang, woog meer dan 2000 ton, was gedecoreerd met marmer en ivoor, en had een bibliotheek, een sportzaal, een zwembad, een kleine tempel gewijd aan Aphrodite, een wandelpad omzoomd met bloembedden, visvijvers, vee- en paardenstallen, een graanopslagplaats, een veelkleurige mozaïekvloer waarop het hele verhaal van Homerus’ Ilias stond afgebeeld, een paar gevechtstorens uitgerust met een katapult, onderkomens voor soldaten en hutten voor zeshonderd passagiers aan boord.

Archimedes zorgde zelf voor zowel de meest geavanceerde bewapening als de archimedische schroefpomp waarmee het schip droog kon worden gehouden, omdat er door het grote oppervlak aan houten huid heel wat water naar binnen lekte.
Eenmaal klaar moest het enorme schip nog te water worden gelaten. Tot verbijstering van de koning – zo gaat het verhaal verder − had Archimedes een systeem van katrollen, hefbomen en schroeven aangelegd waarmee hij van enige afstand in zijn eentje het schip kon lanceren, waarna Hiero de burgers van Syracuse de opdracht gaf ‘in het vervolg alles te geloven wat Archimedes beweerde’. Als de Syracusia zijn volgens de overlevering enige vaart van Syracuse naar Alexandrië ook werkelijk heeft volbracht moet dat als een groot wonder worden beschouwd. Het ligt veel meer voor de hand dat het onbestuurbaar door zijn logheid als een Costa Concordia avant la lettre op de rotsen van de Middellandse Zeekust is gelopen en gekapseisd. Maar het is hoe dan ook volkomen terecht dat ’s wereld eerste, in 1839 in Engeland te water gelaten stoomschip dat met een schroef werd voortgedreven, als eerbewijs de SS Archimedes is genoemd.
Toen hij daar door koning Gelo II om werd gevraagd ontwikkelde Archimedes zelfs oorlogstuig waarmee hij het enorme Romeinse leger twee jaar van Syracuse kon weghouden. De stad lag midden tussen de elkaar tijdens de drie Punische Oorlogen bestrijdende steden Rome en Carthago, en was uit lijfsbehoud soms een alliantie met de ene en dan weer met de andere partij aangegaan. Tijdens de Eerste Punische Oorlog in 263 v.Chr. stapte Hiero II over van Carthago naar Rome, maar toen de vijandelijkheden in 218 opnieuw begonnen en de Carthagese generaal Hannibal Barkas met 37 olifanten de Pyreneeën en de Alpen overtrok en de Romeinen de ene na de andere nederlaag toebracht, sloot Syracuse weer een verbond met Carthago en gaf aan Archimedes de opdracht de verdedigingswerken van de stad tegen de verwachte Romeinse tegenaanval te versterken. Die maakte er zo’n onneembare vesting van, uitgerust met de meest moderne bewapening, dat noch het Romeinse grondleger noch de vloot onder bevel van generaal Marcellus in staat was de stad te veroveren en er geen andere mogelijkheid overbleef dan een langdurige belegering en uithongering, waardoor de stad uiteindelijk viel met het bekende gevolg van Archimedes’ dood.
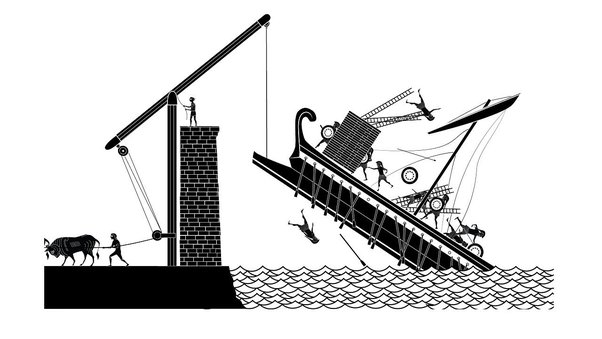
Tot de door hem ontwikkelde wapens waarmee hij de Romeinen zo geen grote verliezen maar dan toch wel grote angst inboezemde en op de vlucht joeg, behoren volgens de overlevering grote katapulten, klauwen en brandspiegels of -glazen. Een klauw of ‘schipschudder’ bestond uit een grote metalen haak die aan een lange houten arm van een kraan was bevestigd en op een naderend schip kon worden neergelaten en vastgehaakt, waarna de arm met takels, katrollen en mankracht werd opgetrokken en het schip met bemanning en al uit het water getild, omgegooid en tot zinken gebracht. In 2005 is er voor de televisiedocumentaire Superweapons of the Ancient World voor Discovery Channel een model van de klauw nagebouwd en bleek het apparaat inderdaad naar behoren te werken.
Over de brandspiegels bestaat meer onzekerheid. De tweede-eeuwse schrijver Lucianus van Samosata beweert dat Archimedes gedurende het beleg van Syracuse Romeinse schepen vernietigde door ze in brand te steken. Drie eeuwen later schreef Anthemius van Tralles dat Archimedes daarvoor brandglazen gebruikte waarmee hij zonlicht op de schepen kon richten en ze zo in vlammen liet opgaan. Omdat Archimedes moeilijk over glazen lenzen of spiegels van die omvang kon beschikken is wel gesuggereerd dat hij daar de koperen schilden van soldaten voor gebruikte, die hij dan in paraboolvorm opstelde. In 1973 heeft de Griekse wetenschapper Ioannis Sakkas op de marinebasis bij Athene dat experiment ook uitgevoerd, waarbij hij zeventig verkoperde spiegels van ongeveer 1 bij 1,5 meter gebruikte, die hij op een scheepsmodel van geteerd triplex op vijftig meter afstand richtte. En jawel, bij de juiste stand van de spiegels vloog het schip na een paar seconden in brand. Latere experimenten, in 2005 en 2010, waaronder die van een groep MIT-onderzoekers op verzoek van het televisieprogramma MythBusters, waren minder succesvol en worden als mislukt beschouwd. In aanmerking genomen dat Syracuse aan de oostkust van Sicilië ligt en de spiegels alleen maar konden werken in de vroege ochtend bij een wolkenloze hemel en met langdurig stilliggende schepen, moeten de conventionele brandende pijlen en met een katapult afgeschoten vuurballen als veel effectiever worden beschouwd om de Romeinse vloot in brand te krijgen. Wel mogelijk is dat de Romeinse soldaten aan boord door het felle licht van de spiegels verblind en in de war raakten, zoals tegenwoordig met voetballers gebeurt die vanaf de publieke tribune met laserpennen worden beschenen.
Omstreeks het jaar 1000 waren de toen nog bekende verhandelingen van Archimedes vastgelegd in twee codices: Codex A en Codex B. Daartoe behoorden Over het evenwicht van vlakken, Over het meten van een cirkel, Over spiralen, Over de bol en de cilinder, Over conoïden en sferoïden, Over drijvende lichamen, Over de kwadratuur van de parabool, Stomachion, Het rundveeprobleem en De zandrekenaar. De rest was vanwege de kwetsbaarheid van papyrus door de tand des tijds verloren gegaan of door ijverige monniken van het dure perkament gekrabd en met religieuze teksten overschreven, als ze al niet als heidense dus waardeloze geschriften in strenge winters in het vuur waren gegooid, dan wel door plunderende en brandstichtende kruisvaarders vernietigd. Groot was dan ook de opwinding en vreugde toen de Deense filoloog Johan Heiberg in 1906 in een bibliotheek in Constantinopel een codex van 174 bladzijden geitenperkament met gebeden ontdekte, waaronder een tekst met zeven verhandelingen van Archimedes verborgen was. Onderzoek met ultraviolet- en röntgenstraling aan dit Archimedes Palimpsest of ook wel Codex C genoemde document bracht naast een aantal reeds bekende teksten ook uniek materiaal aan het licht: een uitgebreidere versie van de Stomachion, een in het originele Grieks gestelde verhandeling Over drijvende lichamen en vooral het verloren gewaande De methode van mechanische stellingen. Vooral deze laatste tekst is bijzonder interessant omdat Archimedes daarin niet alleen de uitkomsten van zijn denkwerk vermeldt maar, wat voor die tijd hoogst ongebruikelijk was, inzicht geeft in de manier waarop hij met vallen en opstaan tot zijn resultaten is gekomen.


Een verslag van de geschiedenissen van de Codices A, B en C zou een thriller opleveren waarnaast Umberto Eco’s De naam van de Roos en Dan Browns De Da Vinci Code volledig in het niet vallen. De documenten zijn regelmatig ternauwernood aan vernietiging ontsnapt, bleven lang verborgen in afgelegen kloosters, zijn in handen van vervalsers gevallen en hebben in de bibliotheken van Alexandrië, Constantinopel, Jeruzalem en in het Vaticaan vertoefd. In 1998 werd de Codex C voor twee miljoen dollar op een veiling van Christie’s in New York verkocht aan een anonieme verzamelaar die zijn fortuin had gemaakt in de informatietechnologie en het twee maanden later voor onderzoek overdroeg aan het Walters Art Museum in Baltimore, maar die het nu, nadat het al zijn geheimen over Archimedes’ aan waanzin grenzende genialiteit heeft prijsgegeven, weer terug heeft.
