– DE MODERNE NATUURKUNDIGE THEORIEËN –

1. Van determinisme naar chaostheorie – 2. Van determinisme naar kwantumtheorie –
3. Ruimte, tijd en relativiteit

Ruimte, tijd en relativiteit

Albert Einstein, de productiefste fysicus van de twintigste eeuw en samen met Aristoteles, Newton en Maxwell behorend tot de beroemdste natuurwetenschappers aller tijden, publiceerde in hetzelfde zijn annus mirabilis genoemde jaar 1905 waarin zijn kwantumtheoretische artikel over het foto-elektrisch effect verscheen, ook nog drie andere baanbrekende artikelen in het toonaangevende tijdschrift Annalen der Physik: een theoretische verhandeling over de Brownse beweging: het op de keukentafel uit te voeren experiment en met met het blote oog zichtbare effect van botsende vloeistofmoleculen op kleine, zwevende deeltjes

en twee artikelen die de derde pijler van de moderne natuurkunde zouden vormen, waarvan het eerste – ‘Zur Elektrodynamik bewegter Körper’ − de beginselen van de speciale relativiteitstheorie bevat en de laatste als consequentie daarvan de gelijkwaardigheid van energie en massa: E=mc².

En net zoals de kwantumtheorie een aanvankelijk gretig door Einstein geaccepteerde tegen-intuïtieve kern heeft die tot uitdrukking komt in het deeltje-golfdualisme en de constante van Planck, zo heeft de relativiteitstheorie een minstens even tegen-intuïtieve, maar ook door Einstein als juist herkende en aangenomen veronderstelling over de lichtsnelheid c als universele natuurconstante, met al even absurde, maar inmiddels steeds meer experimenteel bevestigde gevolgen.

Toen James Clerck Maxwell in 1873 zijn wetten voor elektromagnetische golven publiceerde als schijnbaar solide sluitsteen van de klassieke natuurkunde, was het hem bekend dat deze straling, waaronder zichtbaar licht, een weliswaar zeer hoge, maar toch eindige voortplantingssnelheid heeft van ten naaste bij 300.000 kilometer per seconde. Verder veronderstelde Maxwell dat er een door hem ether genoemd medium moet zijn waardoor licht en andere elektromagnetische golven zich door de ruimte kunnen blijven verplaatsen, ook als de stralingsbron intussen is uitgedoofd − wat om later te verklaren redenen geen correcte gedachte is. Daarom bereikt ons nu iedere nacht nog het miljarden jaren geleden uitgezonden licht van sterren die zelf allang niet meer bestaan, en zijn er intussen legio sterren ontstaan die we op aarde nog niet kunnen zien.

Net zoals geluidsgolven lucht nodig hebben om zich voort te planten, en watergolven water, zo kunnen ook elektromagnetische golven zich niet verplaatsen zonder dat er ‘iets’ is dat kan golven, dacht Maxwell. Het lag voor hem daarom evenzeer voor de hand aan te nemen dat het mogelijk moet zijn de snelheid waarmee de aarde door de ether beweegt − de ‘etherwind’ − te bepalen door het meten van de lichtsnelheid in verschillende richtingen. Het licht van een ster waar de aarde door de jaarlijkse omloop rond de zon door de ether naartoe beweegt moet immers met een grotere snelheid passeren dan het licht van een ster waar de aarde juist vanaf beweegt

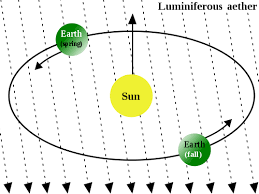
net zoals dat met de snelheid van een passerende tennisbal of geluid het geval is: wie tegen de bewegingsrichting van een tennisbal of het geluid van een sirene inloopt wordt er met een grotere snelheid – hardere klap of hogere toon − door getroffen dan wie met de bal of het geluid meeloopt, en wie even snel of nog sneller mee rent, voelt of hoort zelfs helemaal niets.

Om dit verschijnsel aan te tonen en te meten voerden Albert Michelson en Edward Morley in 1887 een ingenieus, op de interferentie van lichtgolven gebaseerd experiment uit,

waarmee ze echter tegen elke verwachting in aantoonden dat er geen meetbaar verschil bestaat tussen de snelheden van het licht dat de aarde vanuit welke richting dan ook bereikt:

Uit al het voorgaande blijkt met redelijke zekerheid dat de beweging van de aarde en de ether ten opzichte van elkaar, als die bestaat, klein moet zijn,^[1]

schreven Michelson en Morley in uiterst voorzichtige bewoordingen, wat erop neerkomt dat óf de aarde toevallig altijd stil hangt ten opzichte van de ether, óf dat er iets anders vreemds aan de hand moet zijn.

Er waren verschillende fysici, onder wie Henri Poincaré en Hendrik Lorentz, die zich hebben ingespannen om een ‘klassieke’ verklaring te vinden voor dit verrassende fenomeen, maar niet verder kwamen dan geforceerde, dus weinig bevredigende oplossingen. Zo opperde Lorentz het idee dat alle voorwerpen, dus ook het apparaat van Michelson en Morley, in de richting van de ‘etherwind’ verkort worden – net zoals een auto die tegen de wind in rijdt door de grotere luchtdruk wel iets korter zal zijn dan een auto die de wind mee heeft – maar dan op zodanige wijze dat het verschil in de gemeten lichtsnelheid in die richting en in de richting er loodrecht op precies wordt gecompenseerd. Er is dus wel verschil in de lichtsnelheid, veronderstelde Lorentz, maar dat kunnen we vanwege de contractie van onze apparatuur nooit meten, omdat die twee effecten elkaar precies opheffen.

Einstein was degene die het probleem op dezelfde manier ‘oploste’ zoals Niels Bohr dat met zijn kwantumpostulaten voor het atoom had gedaan, namelijk door de constante lichtsnelheid niet te willen begrijpen vanuit de bestaande natuurkunde van Newton en Maxwell, maar door dit klassiek kennelijk onverklaarbare verschijnsel als uitgangspunt te nemen voor zijn relativiteitstheorie: het licht heeft geen ether als drager nodig maar kan zich als een zichzelf genererende afwisseling van veranderende elektrische en magnetische velden door de ruimte verplaatsen, en de snelheid waarmee het dat doet was, is en blijft altijd hetzelfde voor alle waarnemers, in alle richtingen, onafhankelijk van de rust- of bewegingstoestand waarin welke waarnemer dan ook zich bevindt. Of nog anders gesteld: er bevindt zich niet iets in de ruimte dat door de elektromagnetische golf in trilling wordt gebracht, maar het is de ruimte zelf die rimpelt, dat wil zeggen zich periodiek verdicht en verdunt.

Het merkwaardige hiervan is meteen in te zien als we de manier waarop het licht zich verplaatst vergelijken met die van twee andere verschijnselen die wel klassiek te begrijpen zijn: de beweging van een materieel voorwerp en geluidsgolven. Zoals bekend kan een voorwerp zich door de lege ruimte voortbewegen zonder daarvoor een medium nodig te hebben, terwijl geluid zich alleen maar door de atmosfeer kan voortplanten door de aanwezigheid van het medium lucht en is het eigenlijk de trillende beweging van de luchtmoleculen die het geluid transporteert. Stel nu dat we vanuit een rijdende trein in de rijrichting een kogel afschieten. Voor iemand buiten de trein verplaatst de kogel zich met de snelheid waarmee die de loop van het geweer verlaat plus de snelheid van de trein omdat het geweer en de kogel al met de trein meebewegen als het schot afgaat, terwijl het geluid van de knal zich door de voor de waarnemer stilstaande lucht verplaatst met zijn eigen specifieke snelheid, onafhankelijk van die van de trein, het geweer of de kogel. Maar voor de met de trein meebewegende schutter heeft de kogel alleen zijn eigen snelheid, terwijl het geluid bij hem ten achter blijft, omdat de trein zich ten opzichte van de lucht verplaatst. Zou de schutter echter een lichtpistool gebruiken, dan gedraagt het afgevuurde lichtsignaal zich voor hem binnen de trein als een kogel, maar tegelijk voor iemand buiten de trein als geluid, en het is een knap hoofd dat zich een bevredigende klassieke voorstelling kan maken van de dubbele wijze waarop het licht zich tegelijkertijd blijkt te kunnen verplaatsen.^[2]

Op de keper beschouwd betekent het dat de manier waarop het licht zich verplaatst geen eigenschap is van het licht zelf zoals dat met een kogel het geval is, en ook geen eigenschap van het medium zoals bij geluid, maar iets wat inherent is aan de ruimte en de tijd. Einstein ontdekte op zestienjarige leeftijd zelfstandig dat dit al bleek uit de vergelijkingen van Maxwell en dat de aard van elektromagnetische straling inhoudt dat die zich ten opzichte van welke waarnemer dan ook met dezelfde snelheid c moet verplaatsen, wat in die tijd door menigeen – en tegenwoordig nog door een enkeling − zo absurd werd gevonden dat Maxwells vergelijkingen met een korreltje zout werden genomen. Absurd is die eigenschap van de lichtsnelheid nog steeds, maar de vergelijkingen van Maxwell worden niet meer betwijfeld. De vraag die Einstein zichzelf stelde was hoe de wereld en het licht daarin er zouden uitzien als hij met een lichtstraal zou meereizen, en hij kwam toen tot de slotsom dat het licht hem nog steeds met de snelheid c zou moeten passeren. Met andere woorden, de lichtsnelheid opgeteld bij de lichtsnelheid moet weer de lichtsnelheid opleveren: c+c=c, en dat geldt uiteraard ook voor het verschil: c–c=c, wat alleen maar kan betekenen dat de lichtsnelheid geen scalaire grootheid is die net als de natuurlijke getallen bij zichzelf opgeteld of afgetrokken kan worden.

Ook binnen de fysische wereld keek men aanvankelijk vreemd aan tegen de claims van de speciale relativiteitstheorie en bleef het na het verschijnen van ‘Zur Elektrodynamik bewegter Körper’ een tijdje angstig stil. De eerste die Einstein maanden later een brief stuurde met wat vragen van technische aard en ook tijdens zijn colleges aandacht besteedde aan zijn jonge collega uit Bern was Max Planck, die het jaar daarvoor nog hoofdschuddend het artikel van Einstein over het deeltjeskarakter van het licht had gelezen, maar nu toch duidelijk geïnteresseerd was geraakt. Einstein was later zo joviaal om te bekennen dat dat de aandacht die de theorie na de moeizame begintijd ten slotte toch kreeg, voor het belangrijkste deel te danken was aan de warme belangstelling die met name Max Planck ervoor aan de dag had gelegd.^[3]

Speciale relativiteitstheorie: tennissen in Einsteins hogesnelheidstreinen

Om de vreemde consequenties van de op zich simpele aanname van Einstein te kunnen overzien, bedienen we ons ook verder van de spoorwegen − het favoriete vervoersbedrijf van Einstein omdat hij zijn idee voor de speciale relativiteitstheorie naar eigen zeggen peinzend in een Zürichs trein- of tramstel had opgedaan, reden waarom de trein die de verbinding tussen Zürich en Tsjechië onderhoudt naar hem is vernoemd − om met behulp daarvan een paar vergelijkende experimenten uit te voeren met ‘klassieke’ tennisballen en uit ‘relativistische’ deeltjesgolven of fotonen bestaande lichtflitsen.

Precies midden in een stilstaande trein staat een A geheten persoon die op een zeker moment tegelijkertijd twee tennisballen met dezelfde snelheid van x kilometer per seconde (km/sec) weggooit, de ene naar de voorkant en de andere naar de achterkant van de trein. Op hetzelfde moment aangekomen in beide uiteinden kaatsen de ballen tegen de achter- en voorwand en komen uiteraard gelijktijdig weer bij A terug. Een tweede persoon, die we B zullen noemen en die buiten de geparkeerde trein staat maar door de ramen naar binnen kan kijken, ziet precies hetzelfde gebeuren, en als A en B achteraf bij een kop koffie in de stationsrestauratie van gedachten wisselen over wat ze hebben gezien, zullen ze daar geen enkel meningsverschil over hebben. De ruimte kent immers geen voorkeurspunt en wat A vanuit zijn positie met de tennisballen ziet gebeuren, moet er vanaf de positie van B net zo uitzien.

Nu wordt de trein, met nog steeds A en zijn twee tennisballen erin, en B er buiten langs de spoorbaan, op een aanzienlijke snelheid van y km/sec gebracht waarna A, terwijl hij B passeert, dezelfde handelingen verricht: hij werpt een van zijn tennisballen naar voren en tegelijkertijd de andere naar achteren en vangt ze na terugkeer weer keurig op. Voor A zullen de gebeurtenissen er binnen de rijdende trein precies hetzelfde uitzien als met de stilstaande trein, omdat A, de trein en de tennisballen vóór het werpen met dezelfde snelheid y km/sec voortrazen en er onderling of relatief geen verschil bestaat met de begintoestand in de stilstaande trein. Voor B, die langs de spoorbaan staat, ziet het er nu wat anders uit, omdat de snelheid van de trein en de ballen nu, net als bij het geweer en de kogel, moeten worden opgeteld respectievelijk afgetrokken: als A met een snelheid van y km/sec B voorbijrijdt dan gaat de bal die in de rijrichting van de trein wordt gegooid voor B met een hogere snelheid van (y+x) km/sec naar de voorkant van de trein, en de andere, die dus tegen de rijrichting in vliegt, ten opzichte van B met een lagere snelheid van (y-x) km/sec. Maar omdat de trein in de tijd dat de ballen onderweg zijn naar de uiteinden met een snelheid van y km/sec vóór de snelle bal uitrijdt en de langzame bal tegemoet komt, kaatsen ze toch op hetzelfde moment terug, en komen ze ook voor B gelijktijdig weer bij A aan, alleen op een andere ontmoetingsplaats ten opzichte van B, omdat de trein met A erin intussen een stukje is doorgereden. A en B zullen achteraf aan hun koffietafeltje ook nu weer volledig tot overeenstemming komen over tijd én plaats van de gebeurtenissen, als ze maar in aanmerking nemen dat de tennisballen voor elk van hen een verschillende snelheid hebben, veroorzaakt door het rijden van de trein. Ook de snelheid heeft immers alleen relatieve betekenis en kan er bij alle onderdelen van een mechanisch proces een vaste snelheid opgeteld worden zonder dat het proces daardoor verandert.

Een tweede experiment met de tennisballen is van hetzelfde laken een pak, maar wordt nu uitgevoerd in de breedte van de trein. Als A een bal met een snelheid van x km/sec tegen de zijkant van de trein werpt en weer opvangt, zal hij geen verschil vinden tussen het stilstaande en rijdende geval, omdat het voor A en de bal relatief niet uitmaakt of ze allemaal dezelfde zijwaartse beginsnelheid van 0 of van y km/sec hebben. B zal bij de stilstaande trein precies hetzelfde zien als A, evenals in het rijdende geval, als hij dan tenminste weer in aanmerking wil nemen dat de langere weg die de bal volgens hem heeft afgelegd kan worden verklaard met de verplaatsing van de trein: volgens B heeft de bal immers niet alleen zijn eigen snelheid van x km/sec in de breedte, maar ook nog vectorieel daarbij opgeteld de zijdelingse snelheid van y km/sec in de lengterichting van de trein, wat volgens de stelling van Pythagoras uitkomt op een resulterende snelheid van √(x²+y²) km/sec – en veel meer wiskunde dan de stelling van Pythagoras is er in allereerste aanleg voor het begrijpen van de speciale relativiteitstheorie niet nodig.

Nu herhalen we dezelfde serie experimenten nog eens, maar vervangen de tennisballen door twee staaflantaarns waarmee A lichtflitsjes (of fotonen) in beide richtingen kan uitzenden. Zolang de trein stilstaat is er geen essentieel verschil met de tennisballen – behalve dan dat de fotonen veel en veel sneller gaan − en zien A en B precies hetzelfde, maar zo gauw de trein op gang is gebracht beginnen de problemen. A stuurt zijn fotonen met de lichtsnelheid c twee kanten op in de lengterichting van de trein, waarna ze tegelijkertijd aan beide uiteinden gereflecteerd worden en ook weer door A gelijktijdig terug ontvangen. Dat verschilt niet van de tennisballen, dus daar zit het probleem niet, maar voor B is de situatie nu geheel anders, veroorzaakt door Einsteins op de wetten van Maxwell en het experiment van Michelson en Morley gebaseerde stelling dat de fotonen voor A en B, zowel binnen als buiten de rijdende trein, exact dezelfde snelheid moeten hebben en houden, en niet een verschillende zoals dat met de tennisballen het geval was. Voor B gaan de fotonen, net als voor A, allebei met de lichtsnelheid c twee kanten op de trein door, en niet zoals de tennisballen gecorrigeerd voor de snelheid van de trein. Omdat de trein zich intussen verplaatst zal het foton dat tegen de rijrichting in wordt gestuurd volgens B de achterkant van de trein eerder bereiken dan het foton dat met de rijrichting van de trein meevliegt, maar zullen na reflectie wegens het omgekeerde effect wel weer tegelijk bij A aankomen. Het even voor de hand liggende als verbijsterende gevolg is dan dat A en B achteraf bij de volgende kop koffie van mening verschillen over het moment waarop de fotonen de uiteinden van de trein bereikten: volgens A precies tegelijk en volgens B de ene iets eerder en de andere iets later, zodat we moeten vaststellen dat dezelfde gebeurtenissen niet voor iedereen op hetzelfde moment plaatsvinden en er dus voor waarnemers zoals A en B die ten opzichte van elkaar bewegen geen gezamenlijk absoluut referentiekader in de tijd bestaat: het nu-moment voor A – het moment waarop de fotonen de uiteinden van de trein bereiken – is voor B uitgerekt in de tijd.

Herhalen we vervolgens het tweede experiment in de breedte van de trein met fotonen in plaats van tennisballen, dan doet zich de even problematische situatie voor dat B het foton in het geval van de rijdende trein een langere weg ziet afleggen dan A dat ziet: het foton kaatst met een snelheid c tegen de zijwand en terug, net als voor A, maar beweegt ook nog met een snelheid van y km/sec met de trein mee. Omdat dit verschil in afgelegde weg nu niet verklaard kan worden door de treinsnelheid vectorieel bij de snelheid van het foton op te tellen tot √(c²+y²) km/sec − de snelheid ten opzichte van B kan immers niets anders zijn dan c − kunnen we alleen maar vaststellen dat vanuit het gezichtspunt van B de tijd in de rijdende trein trager moet verlopen: voor B loopt het horloge van A langzamer dan voor A zelf, omdat het foton zijn volgens B langere weg toch met dezelfde snelheid in dezelfde tijd moet kunnen afleggen.

Vatten we de resultaten van deze experimenten nog even samen dan moeten we aannemen dat gebeurtenissen die voor iemand in een rijdende trein op hetzelfde moment plaatsvinden voor iemand langs de spoorbaan een spreiding in de tijd vertonen, en dat de klokken in de trein voor iemand erbuiten langzamer lopen dan voor de reiziger die erin zit.

Tijdruimte

Verrichten we nu voor getrainde wis- en natuurkundigen enig elementair, maar voor anderen veelal nog te lastig rekenwerk, dan blijkt het voor de verklaring van al deze verschijnselen ook nodig te zijn dat de rijdende trein voor B langs de spoorbaan korter moet zijn dan voor A die in de trein zit. Dit fenomeen valt ook wel zonder rekenen aanschouwelijk te maken als we aan A in de rijdende trein twee assistenten toewijzen die elk aan een uiteinde van de trein gaan zitten. B spreekt nu met A’s assistenten af dat zij, om de lengte van de trein te bepa­len, een baken uit de trein langs de spoorbaan zullen werpen op het moment dat zij de lichtflits uit A’s lamp ontvangen. Als A’s assistenten dan volgens hun eigen waarneming precies tegelijkertijd hun baken naar buiten gooien, moet de afstand tussen de bakens langs de spoorlijn ook precies gelijk zijn aan de lengte van de trein. Maar B ziet eerst het baken aan de achterkant van de trein naar buiten komen – voor B bereikt de lichtflits de achterzijde van de trein immers eerder – en iets later pas dat aan de voorzijde, wat hem tot de conclusie brengt dat de voorste assistent te lang heeft gewacht en dat de trein daarom in werkelijkheid korter is dan de mensen in de trein hem proberen te laten geloven.^[4] Of beter gezegd: niet de trein is voor B korter in een overigens ongewijzigde ruimte, maar vanuit B’s standpunt is de ruimte die de trein in de lengterichting inneemt korter.

Terwijl voor A en zijn assistenten de reflectie van de fotonen op exact hetzelfde moment plaatsvindt en de trein, rijdend of stilstaand, uiteraard gewoon zijn lengte L behoudt, staat het voor B vast dat de gebeurtenissen in de trein een zekere uitgebreidheid in de tijd (∆t) vertonen – het ene foton bereikt de achterzijde van de trein eerder dan het andere de voorzijde − terwijl de lengte afneemt van L tot L-ΔL=L’. Verdere experimenten in die richting tonen ook nog aan dat deze effecten sterker worden als de snelheid van de trein toeneemt: hoe sneller de trein rijdt, hoe korter hij voor buitenstaanders wordt en hoe groter het tijdverschil tussen de voor inzittenden gelijktijdige gebeurtenissen in de voor- en de achterkant van de trein. Wél maakt enig cijferwerk met de stelling van Pythagoras duidelijk dat, als de spreiding in de tijd ∆t en de lengte L’ van de rijdende trein vectoriëel – in de zogenaamde Minkowskiruimte − bij elkaar worden opgeteld, dat dan hoe snel de trein ook rijdt in alle gevallen de waarde van L eruit komt: √(∆t²+L’²)=L. Terwijl in de klassieke natuurkunde de ruimtelijke afmetingen bij beweging voor iedere waarnemer hetzelfde zijn en de gebeurtenissen op scherp bepaalde momenten in de tijd plaatsvinden, blijken tijd en ruimte in de relativistische natuurkunde met elkaar verbonden te zijn en zich samen te voegen tot tijdruimte, en wat constant blijft is nu niet de lengte, maar de vectoriële som van de uitgestrektheid in de ruimte en de spreiding in de tijd. Niet dat de ruimte en de tijd daarmee identieke dimensies zijn geworden, omdat het zo blijft dat we ieder punt van de ruimte naar eigen goeddunken kunnen betreden en dus ook naar een vorige plaats kunnen terugkeren, terwijl het verleden voor ons een eens en voor altijd dichtgeslagen boek blijft en de toekomst zich aan ons openbaart in haar eigen tempo – de tijd kan voor een waarnemer van een bewegend systeem daar wel langzamer verlopen maar niet omkeren.

Wederkerigheid

Bij hun verdere onderzoekingen naar de eigenschappen van de in de newtoniaanse mechanica zo eenduidige ruimte en tijd, komen A en B ook nog te weten dat de verkorting van de ruimte en de vertraging en spreiding van de tijd wederkerig zijn. Als A en B elkaar in ieder hun eigen trein tegemoet rijden en passeren, dan is niet alleen A’s trein volgens de waarneming van B korter, maar ook de trein van B in de ogen van A. En niet alleen loopt volgens B het horloge van A langzamer dan die van hemzelf, maar ook B’s horloge volgens A, terwijl hun eigen horloges volgens A en B volstrekt normaal blijven lopen en hun eigen trein zijn normale lengte behoudt. Geïnspireerd door dit natuurkundige verschijnsel noteert de dichter Rogi Wieg in zijn ‘Dagboek van een bloem’:

Hoe is het dat als jij beweegt
ik je klokje trager zie dan dat
van mij en dat jij symmetrisch, als
twee groeiende zonnebloemen in een raam,
mijn klokje ook vertraagd ziet
lopen tussen de gebeurtenissen
van liefde dood en relativiteit.^[5]

Met de wederkerigheid van de verschijnselen onderscheidt Einsteins theorie zich van de contractie bij beweging zoals Lorentz zich die voorstelde, omdat de laatste ervan uitging dat de verkorting ten gevolge van de etherwind geen relatief maar absoluut verschijnsel is en voor iedereen – zowel voor de inzittenden als de buitenstaanders van de trein − hetzelfde moet zijn. Lorentz zat met zijn idee de speciale relativiteitstheorie wel op de hielen, maar kwam voor de laatste stap net enige verbeeldingskracht tekort, gezien een door hem in 1913 – toen verreweg de meeste fysici al overstag waren gegaan − uitgesproken tekst:

Deze spreker vindt een zekere bevrediging in de oudere interpretatie, volgens welke de ether ten minste enige mate van substantie heeft, ruimte en tijd duidelijk van elkaar gescheiden kunnen worden, en gelijktijdigheid geen nadere specificatie behoeft. Ten slotte moet worden opgemerkt dat de gewaagde stelling dat men nooit snelheden groter dan de lichtsnelheid kan waarnemen, ons theoretische beperkingen oplegt die niet zonder enige reserve aanvaard kunnen worden.^[6]

Wie moeite heeft met de absurde consequenties van de speciale relativiteitstheorie bevindt zich dus in goed gezelschap maar zal er, zoals het zich nu laat aanzien, toch mee moeten leren leven.

Zetten we de relativistische effecten van twee identieke, elkaar met constante snelheid passerende treinen nog eens op een rij dan blijkt dat vanuit welke trein we ook kijken de andere altijd korter is dan de eigen, de klokken in de andere trein langzamer lopen, en de klok aan de voorkant van de andere trein altijd achterloopt bij die aan de achterkant. Het dient daarbij benadrukt te worden dat hier geen sprake is van zinsbegoocheling of suggestie, en dat de trein van A zich voor B niet voordoet alsof hij korter is en dat het niet alleen maar lijkt alsof A’s horloge voor B langzamer loopt. Wat Einstein zich realiseerde, en wat wij dus ook moeten doen, is dat afmetingen en tijdsintervallen die we in de wereld buiten ons waarnemen geen vaste, onaantastbare waarden vertegenwoordigen die altijd en overal voor iedereen hetzelfde zijn, zoals dat met de ruimte en de tijd van Newton het geval is, maar afhangen van onze relatieve snelheid. Dat we in het dagelijkse leven niets van dit soort verschijnselen merken heeft uitsluitend te maken met de traagheid waarmee alle voor ons direct waarneembare processen verlopen in vergelijking met de lichtsnelheid. Zelfs de langste TGV op de topsnelheid van zeg 500 kilometer per uur zal nog geen fractie van een millimeter verkorten, en de horloges van de passagiers nog geen fractie van een milliseconde vertragen. De effecten worden pas merkbaar bij snelheden die een aanzienlijk deel van de lichtsnelheid bedragen en daar zijn ook de experimentele bewijzen voor Einsteins gelijk te vinden. Zoals het volgende: er bestaan elementaire deeltjes die zeer instabiel zijn en daarom een evenzeer korte levensduur hebben. Als zo’n deeltje ontstaat dan kan dat volgens de wetten van de klassieke natuurkunde, ondanks de hoge snelheid die het heeft, maar een paar centimeter afleggen voordat het weer verdwijnt door uiteen te vallen. Metingen wijzen nu uit dat zo’n deeltje toch een paar meter kan afleggen, en de enig mogelijke verklaring hiervoor is de aanzienlijke vertraging die de inwendige klok van het deeltje door zijn hoge snelheid voor ons ondervindt. Volgens het wederkerigheidsprincipe is het voor het deeltje zelf de verkorting van onze ruimte die de afgelegde weg langer maakt dan op basis van de klassieke in­stabiliteit alleen te verwachten is, maar hoe dan ook, in beide gevallen bereikt het deeltje over een afstand van meters en niet van centimeters de detector. Dat wil dus tevens zeggen dat, als A en B aan de koffietafel van mening verschillen over wat ze hebben gezien, niet een van beiden of allebei aan zinsbegoocheling hebben geleden, maar dat beiden vanuit hun eigen perspectief het gelijk over de lengte van de trein en de spreiding van de gebeurtenissen in de tijd ook werkelijk volledig aan hun zijde hebben. Een conclusie die ontwrichtend genoeg is om ziek van te worden en dan niet als gevolg van de overmaat aan koffie die nodig was om zover te komen.

Net zoals in de paragraaf over Immanuel Kant – zie hoofdstuk VII − de vraag gesteld kon worden of diens kwalitatieve idee van de aan ons bewustzijn inherente tijd- en ruimtecategorieën op enigerlei wijze in overeenstemming is te brengen met de wiskundig kwantitatieve wijze waarop onze bewuste waarneming volgens Einstein de dimensies en de tijd van de dingen en de gebeurtenissen in de Minkowskiruimte beïnvloedt, is hier natuurlijk de omgekeerde vraag op zijn plaats of we de relativistische vergelijkingen van Einstein kunnen beschouwen als de wiskundige invulling van Kants kwalitatieve idee. Immers, ook Einstein beschouwde onze uit het bewustzijn voortkomende ervaring van afgezonderd te zijn van de werkelijkheid als ‘een soort optische misvatting’ en de voortgang van de tijd als een illusie. Einstein heeft Kants werk zeker gelezen, had er ook grote bewondering voor, en had geen goed woord over voor degenen die met de inhoud van de Kritieken kritiekloos aan de haal gingen, wat duidelijk blijkt uit de opmerking die hij maakte tegen medebewonderaar Ilse Rosenthal, waarin hij het werk van Kant beschrijft als ‘een landweg met vele mijlpalen, waar de kleine hondjes die er langslopen hun plasje tegen plegen te deponeren’.^[7] Toch is het opmerkelijk dat neokantiaans genoemde filosofieën als die van Heinrich Rickert en Ernst Cassirer, waarin geprobeerd wordt de ideeën van Kant en Einstein te verenigen, zich tegenwoordig in weinig belangstelling mogen verheugen.

E=mc²

Maar we zijn er nog niet wat de voor ons zo vreemde verschijnselen betreft die de speciale relativiteitstheorie blootlegt. Als we botsingsprocessen tussen elementaire deeltjes – of zeer snel rijdende treinen − bij ons onderzoek betrekken en de vertraging van de tijd door de beweging verdisconteren in de impulsbehoudswet van de klassieke mechanica, dan blijkt dat we ook nog moeten aannemen dat de massa van de deeltjes – of de treinen − geen onder alle omstandigheden vast gegeven meer is, maar bij hogere snelheden groter wordt en bij het benaderen van de lichtsnelheid zelfs naar oneindig groeit. Lorentz’ bedenkingen ten spijt betekent het in feite dat niets sneller kan gaan dan het licht, omdat er geen kracht groot genoeg is om een (bijna) oneindig zware massa nog verder te versnellen. De beperking dat niets sneller kan gaan dan licht bevat ook de onverenigbaarheid met de kwantumtheorie, omdat de kwantumverstrengeling (zie vorige paragraaf) een ‘oneindig snelle’ uitwisseling van informatie betekent, wat volgens Einsteins relativiteit is uitgesloten. Kijken we ook nog naar de klassieke energiebehoudswet, dan volgt daaruit Einsteins beroemdste formule die zelfs iedere dichter foutloos kan opdreunen en die hij in het vierde artikel uit 1905 behandelt: E=mc².

Maar kunnen opdreunen is nog iets anders dan begrijpen. Wordt de wet bij voorkeur verkeerd geïnterpreteerd als de mogelijkheid om massa om te zetten in energie, is de eigenlijke betekenis de gelijkwaardigheid van massa en energie: als we water op het gas zetten en aan de kook brengen dan neemt de (warmte)energie, en dus ook de massa van het water toe; als we ons inspannen om een springveer of een elastiekje uit te rekken dan neemt de (potentiële) energie, dus ook de massa van de veer of het elastiekje toe; als we met kracht een steen wegslingeren dan neemt de (kinetische) energie, dus de massa van de steen toe. Kortom: massa en energie zijn verschillende manifestaties van één en hetzelfde, en als we de totale energie van een systeem willen weten, hoeven we slechts de massa te meten en die met het kwadraat van de lichtsnelheid te vermenigvuldigen. Wél is het zo dat de massa een zeer geconcentreerde vorm van energie is, wat wil zeggen dat een kleine hoeveelheid massa, vanwege de vermenigvuldigingsfactor c² aan de massakant van de formule, overeenkomt met of gelijkwaardig is aan een grote hoeveelheid energie, wat zijn toepassing vindt in kerncentrales en –wapens: als gevolg van kernreacties verdwijnt er een geringe hoeveelheid massa wat gelijkwaardig is aan een enorme hoeveelheid energie, wat Einstein in zijn brief aan president Roosevelt tot zijn correcte voorspelling bracht dat slechts één zo’n bom in staat zou zijn een hele haven en het omliggende gebied van de aardbodem weg te vagen.

Ook voor het aangroeien van massa als gevolg van snelheidsvermeerdering geldt dat we er pas iets van merken als we in de buurt van de lichtsnelheid komen. Zelfs bij de hoogste aardse snelheden van vliegtuigen, kogels of raketten, is het effect verwaarloosbaar klein. Een straalvliegtuig dat aan de grond honderd ton weegt, neemt bij een normale kruissnelheid van duizend kilometer per uur voor de thuisblijvers nog geen tiende milligram in gewicht toe. Wel doet het verschijnsel zich weer aantoonbaar voor in deeltjesversnellers, machines waarin de kleinste materiedeeltjes kunnen worden opgezweept tot een tempo dat aardig in de buurt komt van de lichtsnelheid, waardoor ze inderdaad aanzienlijk in massa toenemen. Een deeltje dat rondvliegt met 99,9 procent van de lichtsnelheid blijkt volgens meting met een massaspectrograaf al meer dan twintig keer zwaarder dan een rustende soortgenoot. Maar waar we al bang voor waren geldt ook nu weer: het verschijnsel is wederkerig. Voor het deeltje zelf is zijn toestand volstrekt normaal, en zal de massa van de razendsnel ronddraaiende massaspectrograaf enorm zijn toegenomen.

Algemene relativiteitstheorie: gewichtloos en jong in de ruimte

De enige beperking die Einstein naast de constante lichtsnelheid aan zijn relativistische treinen opgelegde is dat ze zich met een eveneens constante snelheid ten opzichte van elkaar moeten voortbewegen. Als ook snelheidsveranderingen worden toegelaten, dat wil zeggen als zich versnellingen mogen voordoen, verandert de speciale relativiteitstheorie in de tien jaar later, in 1915, ook door Einstein geformuleerde veel ingewikkelder algemene relativiteitstheorie. Hoeveel ingewikkelder mag blijken uit de raad die Max Planck – intussen allang overtuigd van de juistheid van de speciale relativiteitstheorie – aan Einstein gaf, toen die nog met de wiskunde van zijn nieuwe theorie aan het worstelen was: ‘Als oudere vriend moet ik je adviseren om er een punt achter te zetten, want op de eerste plaats zal het je niet lukken, en als het je al lukt, zal niemand je geloven.’^[8] De waarschuwingen van oudere wis- en natuurkundigen aan het adres van hun driestere jonge collega’s over de gevaren van hun avontuurlijke geestelijke bezigheden waren in die tijd sowieso niet van de lucht.

Het is een van de onbegrijpelijkheden van de fysische wereld dat versnelling een fundamentelere rol speelt dan snelheid. De dichter Rogi Wieg waarschuwt:

Haal nooit snelheid en versnelling
door elkaar! Het relatieve wordt
dan speciaal, of omgekeerd. Verschillende
geraniums blijven wel bloemen, maar
hun plaatsten in het raam staan niet vast.
De een leeft in de toename van snelheid,
de ander gaat eenparig voort. Dat geeft
verschil. Wees voorzichtig met je woorden,
weeg ze, ze worden zwaarder te herstellen
als ze snel je mond verlaten. Hun massa
neemt toe, ze krommen zelfs de ruimte maken
het zo moeilijk om het later goed te zeggen.^[9]

Als we ons alleen in een verder volkomen lege ruimte bevinden is het niet mogelijk om uit te maken welke snelheid we hebben. Er bestaat geen absolute ruimte, dus ook geen absolute snelheid van nul km/sec of welke andere waarde dan ook. Als Robby Egberts, de hoofdpersoon uit A.F.Th. van der Heijdens roman Weerborstels, in een donkere, maanloze nacht aan de hem achtervolgende politie wil ontkomen, dooft hij de lichten van zijn auto, waardoor hij in de totale duisternis schijnbaar al zijn snelheid verliest:

Wat betekende snelheid nog als er niets overbleef ten opzichte waarvan je snelheid kon ontwikkelen? Door het uitschakelen van de verlichting werd Robby’s snelheid, hoe hoog opgevoerd ook, plankgas, als het ware opgeheven. Hij had het gevoel dat hij de pedalen van een orgel bewerkte: ondanks het gierende geluid stond de auto net zo roerloos midden in de nacht als het orgel in een hoge donkere kerk.^[10]

Door de afwezigheid van beweging komt de boom waar de auto van Robby zich na het missen van een bocht in zware plooien omheen drapeert onverwacht met een ruk uit het niets tevoorschijn, toevallig precies op de plek waar de auto zich in het aardedonker bevindt:

Plotseling groeide er, hoog opschietend, een boom uit de auto. Hij was met veel geweld van stam en takken in één ruk dwars door chassis en koetswerk van het in de nacht stilstaande voertuig heen gedrongen. Door de kracht van zijn groei lieten twijgjes en blaadjes los, maar nog voor die konden neer regenen op wat er van de auto restte, stoven er met fluitende vleugelslag twee vogels uit de kruin verschillende kanten op.^[11]

Beweging doet zich alleen maar voor ten opzichte van iets anders. Voor ons aardbewoners, die de hele dag omringd zijn met van alles dat zich met allerlei in verhouding tot de lichtsnelheid onbetekenende snelheden verplaatst, aan wie de werkelijkheid zich voordoet als een permanent rond een archimedisch rustpunt wervelende kermis, is zo’n idee van betekenisloze snelheid aan de basis van ons bestaan toch even wennen. Versnelling – of snelheidsverandering − heeft daarentegen wel een absoluut karakter en iedere snelheidsverandering in een geheel lege ruimte is door ons te voelen en te meten.

Om duidelijk te krijgen waarmee de algemene relativiteitstheorie zich van de speciale onderscheidt, moet het assortiment aan vervoermiddelen worden uitgebreid met een lift of de grote broer daarvan: een ruimteraket. Het was Einsteins fundamentele inzicht dat als astronauten zich in een raket bevinden die door werkende motoren wordt voortgestuwd, zij een ervaring hebben die vergelijkbaar is met wat ze ondervinden in het zwaartekrachtveld van de aarde: door de versnelling van de raket worden de astronauten net zo in hun zetels gedrukt als thuis in hun bureaustoel achter hun werktafel of op de bank voor de televisie. Worden de raketmotoren uitgezet, dan beweegt het ruimteschip zich met constante snelheid verder en komen de astronauten in een toestand van gewichtloosheid terecht. Vergelijkbaar daarmee is dat het voor iemand die zich in een gesloten lift bevindt, zonder zicht op de omgeving, niet mogelijk is om een onderscheid te maken tussen een stilstaande lift in een zwaartekrachtveld, of een opwaarts versnellende lift in een verder krachtenvrije ruimte. Vandaar dat Einstein de boude stap durfde te zetten zwaartekracht en versnelling fysisch identiek te verklaren: wij worden niet aan de aarde gekluisterd door een mysterieuze kracht die massa’s door de lege ruimte heen op elkaar uitoefenen, zoals Newton moest aannemen, maar omdat we ons in een versneld systeem bevinden. Dat iemand die, zoals een parachutespringer vóór hij zijn valscherm opent, vrij valt de zwaartekracht niet voelt en zich daardoor gewichtsloos waant, noemde Einstein ‘de gelukkigste gedachte uit mijn leven’.

Het verschil tussen Newtons en Einsteins mechanica is geen louter formele kwestie. Einsteins interpretatie van de zwaartekracht als versnelling verklaart bijvoorbeeld dat alle voorwerpen − loden kogels en zwanendonsjes − in vacuüm even snel vallen, of in fysische termen, dat de ‘zware’ en de ‘trage’ massa van een voorwerp hetzelfde zijn, wat in Newtons theorie alleen maar als een wonderlijke toevalligheid kan worden gezien. Want waarom zou de kracht waarmee we een voorwerp kunnen behoeden in het aardse zwaartekrachtveld (met een versnelling van bijna 10 meter/sec²) omlaag te vallen, dezelfde zijn als de kracht die nodig is om dat voorwerp met dezelfde versnelling over een horizontaal, ideaal glad oppervlak van zijn plaats te duwen, als zwaartekracht en versnelling niet equivalent zouden zijn? Nog anders gezegd: in Newtons systeem wordt een loden bal harder aangetrokken door de aarde dan een zwanendonsje, maar is door zijn grotere traagheid moeilijker van zijn plaats te krijgen. Beide effecten − zwaarte en traagheid − werken tegengesteld en heffen elkaar toevallig precies op, zodat alle voorwerpen die tegelijk vanaf dezelfde hoogte worden losgelaten ook tegelijk op de vloer terechtkomen − in het luchtledige tenminste. Volgens Einstein werkt er op de in vacuüm losgelaten voorwerpen juist geen kracht zodat ze ten opzichte van elkaar niet van hun plaats komen en is het de vloer die de versnelling ondergaat en de beide voorwerpen uiteraard tegelijkertijd bereikt, waarna ze door de vloer uit hun natuurlijke, krachtenvrije toestand worden gebracht en mee versneld.

Het moeilijk voorstelbare karakter van Einsteins zwaartekracht als versnelling blijkt onder andere uit het meestal goed doordachte werk van Jules Verne. Bij een beschrijving van een reis naar de maan in een soort reusachtige kanonskogel veronderstelt Verne onderweg maar één moment van gewichtloosheid, namelijk als de kogel zich precies bevindt op het punt waar de zwaartekracht van de aarde en de maan elkaar opheffen.

Maar, zoals hiervoor al gezegd, weten we uit onze ervaringen met de ruimtevaart inmiddels dat, zo gauw de raketmotoren zijn uitgezet, of zo gauw de kogel de loop van het kanon heeft verlaten, de astronauten en de rest van het interieur van het ruimteschip zich de hele verdere reis in gewichtloze toestand bevinden tot de kogel inslaat op het oppervlak van de maan, of tot de motoren weer worden aangezet om dat te voorkomen en een zachte landing te bewerkstelligen.

Blijft nog de vraag of we ons een handzame voorstelling kunnen maken van hoe planeten, kometen en manen in hun baan rond de zon en de planeten blijven, meteoren op planeten en manen kunnen inslaan, en wij met onze beide benen op de grond blijven zonder dat we daarvoor Newtons op magie berustende aanname van de zwaartekracht nodig hebben. Einsteins verklaring is dat de aanwezigheid van een massa, zoals de zon of de planeten, ter plaatse een ‘kromming’ of ‘verdichting’ in de vierdimensionale tijdruimte veroorzaakt. Planeten bewegen dan ook niet ten gevolge van de zwaartekracht in een elliptische baan om de zon in een homogene, isotrope of ‘rechte’ ruimte zoals Newton dat zag, maar ze volgen hun eigen kortste ‘natuurlijke’ weg door de tijdruimte die door de massa van de zon is gekromd, en daarvoor is dus juist geen kracht nodig. Een mogelijk verhelderend model van een dimensie minder en daarom voor ons beter voorstelbaar is een als een biljartlaken horizontaal strak gespannen rubberen vel – een tweedimensionale ‘rechte’ ruimte − waar aan de onderkant hier en daar aan haakjes gewichten zijn opgehangen die trechtervormige deuken in het vel veroorzaken. De vorm − breedte en diepte − van de trechters hangt af van de grootte van de gewichten en kan beschouwd worden als driedimensionale kromming van een tweedimensionale ruimte, als analogon voor de vierdimensionale trechters die massa’s in de driedimensionale ruimte veroorzaken. Laten we nu een balletje met enige snelheid en zonder weerstand over het rubberen vel rollen, dan volgt dat ‘vanzelf’ een slingerende weg langs en rond de verschillende trechters, kan dat in bijzondere gevallen in een vaste elliptische baan om een trechter terechtkomen, en er soms definitief in gevangen worden, net zoals dat het geval is met planeten, manen, kometen en meteoren die zich door de vierdimensionale krommingen van de tijdruimte bewegen.

En ook onze gebondenheid aan de aarde betekent niets anders dan dat we zijn gevangen in de trechter die de massa van de aarde in de vierdimensionale tijdruimte veroorzaakt. En omdat de tijd onder in de trechter het langzaamst verloopt (zie later) kan ook gesteld worden dat zwaartekracht identiek is aan het streven naar de situatie waarin de tijd het traagst verloopt^[12] − en dat uiteindelijk alle materie in zwarte gaten zal zijn verdwenen omdat daarin de tijd tot stilstand is gekomen.

Platlanders

Een idee van de eigenlijk onvoorstelbare gekromde vierdimensionale tijdruimte is wel te vormen als we, zoals de Engelse schoolmeester Edwin Abbott in zijn boek Flatland heeft gedaan,

de tijdas voor de gelegenheid even vervangen door een ‘gewone’ ruimtelijke dimensie en dan de situaties die zich in die vierdimensionale geometrische ruimte aan ons driedimensionale mensen kunnen voordoen inzichtelijk maken door die te vertalen naar de belevenissen van tweedimensionale mensen in een driedimensionale ruimte.

Stellen we ons tweedimensionale mensen – ‘Platlanders’ − voor die wonen op het driedimensionale, gesloten bolvormige oppervlak van een ballon of een planeet, dan ervaren die mensen wel het platte oppervlak waarover ze zich onbeperkt naar alle kanten kunnen bewegen, maar de kromming van het oppervlak in de derde dimensie ontsnapt aan hun waarneming.^[13]

Als ze hebben besloten een lange wandeltocht te ondernemen en ze zich sindsdien steeds verder van hun vertrekpunt hebben verwijderd, wie schetst dan hun verbazing als ze op een dag voetafdrukken aantreffen die bij nadere inspectie van henzelf afkomstig blijken te zijn. Zonder dat ze dat merkten heeft de kromming van het boloppervlak in de derde dimensie ze bij hun uitgangspunt teruggebracht. Sterker nog, als ze lang genoeg hebben rondgewandeld in de volgens hun waarneming vlakke, tweedimensionale wereld zullen ze uiteindelijk overal waar ze komen hun eigen voetstappen aantreffen. Terwijl ze in hun belevenis alleen maar steeds verder zijn weg ­gereisd zonder ooit ergens een grens te zijn tegengekomen, blijken ze overal al geweest te zijn. Er is zelfs een punt op het boloppervlak dat het verste van hun vertrekpunt is verwijderd – zoals de Noordpool het verst is verwijderd van de Zuidpool – en van waaruit ze altijd dichter naar hun vertrekpunt terugkeren, welke kant ze ook opgaan.
Waarderen we dit schouwspel één dimensie op en beschouwen we nu de trektocht van driedimensionale mensen − Bollanders − zoals wij in een ruimteschip door een ruimte die in de vierde dimensie is gekromd, dan begrijpen we de verbazing als ook die mensen ontdekken bij hun oorspronkelijke vertrekpunt te zijn teruggekeerd, terwijl ze het idee hadden steeds verder te zijn weggevlogen. Ook zij kunnen alle plaatsen in de ruimte bezocht hebben zonder ooit een grens te hebben bereikt, zodat we die ruimte – net zoals de Platlanders hun boloppervlak − onbegrensd en in zichzelf besloten kunnen noemen, en ook zij zullen vanuit een ‘verste’ punt alleen maar dichter bij huis kunnen komen, in welke richting ze zich ook begeven. Vandaar dat astronomen kunnen zeggen dat, hoewel er nooit een grens zal worden bereikt, de ruimte van het universum beperkt is en er, vergelijkbaar met de voetstappen in het tweedimensionale geval, niet meer dan een bepaald aantal sterrenstelsels in blijkt te passen, zij het een zeer groot aantal.

In ieder geval is met de vierdimensionale in zichzelf gekromde tijdruimte het probleem van de eindigheid of oneindigheid van ons universum opgelost. Een driedimensionale ruimte die zich oneindig naar alle kanten uitstrekt is onmogelijk voor te stellen, maar een eindige ruimte zorgt ook voor onoplosbare problemen, zoals de pythagoreeër Archytas in de vijfde eeuw voor Christus zich, volgens Lucretius, al bewust was:

Laten we even aannemen dat het universum begrensd is. Als een man de uiterste grens bereikt en een snelle speer werpt, zou die met grote kracht weggeslingerde speer dan nog verder weg vliegen of stuit hij op een of andere barrière, wordt hij in zijn vlucht gestuit?^[14]

Onze vierdimensionale tijdruimte zou volgens deze theorie, vergelijkbaar met het boloppervlak in het driedimensionale geval, in zichzelf besloten en dus tegelijk eindig en onbegrensd kunnen zijn.

De meetkunde van de vierdimensionale tijdruimte

Een wat onverwachte eigenschap voor iemand die als de geestelijke vader van zowel de speciale als algemene relativiteitstheorie moet worden beschouwd en een fundamentele bijdrage aan de kwantumtheorie heeft gegeven is dat Einstein geen bijzonder talent voor wiskunde had. Maar met name zijn vroegere hoogleraar in dat vak, Hermann Minkowski, heeft hem bij geval van het juiste wiskundige instrumentarium voorzien.

Hoewel Minkowski zijn student ‘een luie hond die te beroerd was om colleges te volgen’ had genoemd, was hij in 1905 toch als een van de eersten onder de indruk van de briljante wijze waarop Einstein licht, beweging, tijd en ruimte met elkaar in verband bracht. In de jaren daarna zette Minkowski zich aan de wiskundige analyse van wat Einstein in zijn theorie nu eigenlijk stelt en kwam toen tot de ontdekking dat de verbanden die hij afleidt tussen de lengte en tijdsduur volgens de verschillende bewegende waarnemers eenvoudig kunnen worden begrepen door de tijd en de drie richtingen in de ruimte als één vierdimensionale (Minkowski)ruimte op te vatten.^[15] Einstein was zelf niet zo enthousiast voor deze zuiver wiskundige benadering en noemde het ‘overbodige geleerderigheid’ die alleen maar tot gevolg had dat hijzélf niets meer van de relativiteitstheorie begreep.

Ook de veel ingewikkelder algemene relativiteitstheorie plaatste Einstein voor onoverkomelijke wiskundige problemen, maar nu was het Marcel Grossmann, een van zijn vroegere medestudenten, die hem de juiste weg wees.^[16]

Grossmann was bekend met de wiskunde van de gekromde ruimte en begreep meteen dat de meetkunde van de Duitse wiskundige Bernhard Riemann, waarin de kromming van de ruimte in elk punt wordt aangegeven door een hele matrix van getallen, de oplossing van Einsteins problemen inhoudt.^[17] Einstein had dus het geluk dat toen hij zijn algemene relativiteitstheorie ontwikkelde, de daarvoor benodigde wiskunde in de eeuwen daarvoor al was ontworpen, en het is uit serendipistisch oogpunt interessant eens na te gaan hoe dat historisch in zijn werk is gegaan.

Het eerste belangrijke werk op het gebied van de meetkunde van het platte vlak is het door Euclides circa 300 v.Chr. geschreven Elementen. Daarin formuleert hij de vijf uitgangspunten of postulaten waarmee ook ieder hedendaags leerboek voor de vlakke of euclidische meetkunde nog begint. In wat moderner bewoordingen luiden deze: 1. Vanuit ieder punt in een vlak kan één rechte lijn worden getrokken naar ieder ander punt in dat vlak; 2. Een rechte lijn kan naar beide kanten willekeurig ver verlengd worden; 3. Om ieder punt kan een willekeurig aantal cirkels beschreven worden; 4. Alle rechte hoeken zijn gelijk; en 5. Door een punt buiten een rechte lijn gaat maar één rechte lijn die evenwijdig is aan de eerste rechte lijn.

Deze postulaten werden door Euclides en vele wiskundigen en filosofen na hem tot en met Spinoza en Kant als onbewijsbaar, maar intuïtief als onbetwijfelbaar juist beschouwd en alle andere minder voor de hand liggende eigenschappen van figuren in het platte vlak en in de rechte ruimte, zoals de stelling van Pythagoras en de stelling dat de som van de hoeken van een driehoek 180⁰ bedraagt, zijn eruit af te leiden. Wil zo’n verzameling postulaten een correcte basis voor een wiskundig sys­teem vormen, dan mag er niets te weinig en niets te veel in staan. Als er te weinig in staat kunnen niet alle eigenschappen van figuren in het platte vlak of in de rechte ruimte eruit worden afgeleid en moet er een nieuw postulaat aan worden toegevoegd, en als er te veel in staat kunnen een of meerdere van de postulaten uit de andere worden afgeleid en zijn dan als postulaat overbodig.^[18] Hoewel het systeem van Euclides eeuwenlang als hét voorbeeld van zuiver wiskundig denken is beschouwd, is er ook wel getwijfeld aan de noodzakelijkheid van het vijfde postulaat en kwam een van de grootste wiskundigen aller tijden Carl Friedrich Gauss in 1815 tot de conclusie dat er ook een logisch consistente meetkunde te formuleren is die dat postulaat niet nodig heeft. Maar hij vond dat resultaat te merkwaardig om te publiceren – méér dan één rechte lijn door een punt evenwijdig aan een andere rechte lijn − uit angst door zijn tijdgenoten belachelijk gemaakt te worden. Meer dan tien jaar later werden dezelfde, nog steeds als hoogst twijfelachtig beschouwde resultaten tegelijkertijd herontdekt en openbaar gemaakt door de Rus Nikolaj Lobatsjevski en de Hongaar János Bolyai. De eerste vond zijn meetkunde zo vreemd dat hij het ‘imaginaire meetkunde’ noemde, en de laatste deed zijn wiskundige onderzoek – ‘Uit niets heb ik een vreemd, nieuw universum geschapen’− tegen het uitdrukkelijke advies van zijn vader Wolfgang in:

Houd er in vredesnaam mee op. Het is een even groot kwaad als zinnelijke hartstocht, want je kunt er zodanig door worden meegesleept dat je je gezondheid, je gemoedsrust en je levensgeluk op het spel zet.^[19]

Helemaal zonder eigenbelang was dat advies van vader Bolyai niet, omdat hij, zelf ook wiskundige, een groot deel van zijn leven aan het bewijs van Euclides’ vijfde stelling had besteed en het niet prettig vond om te horen dat die helemaal niet nodig was. Maar nu was het Gauss zelf die de oude Bolyai, met wie hij bevriend was, ervan wist te overtuigen dat wat zijn zoon deed niet zo vreemd was, omdat hij daar zelf ook jaren mee bezig was geweest, waarop Wolfgang besloot het baanbrekende werk van zijn zoon op te nemen als bijlage in een boek van hemzelf dat hij in 1832 publiceerde. Na de dood van Gauss in 1855 bleek uit diens dagboek dat hij de eerste was geweest die zijn niet-euclidische ideeën had genoteerd.^[20]

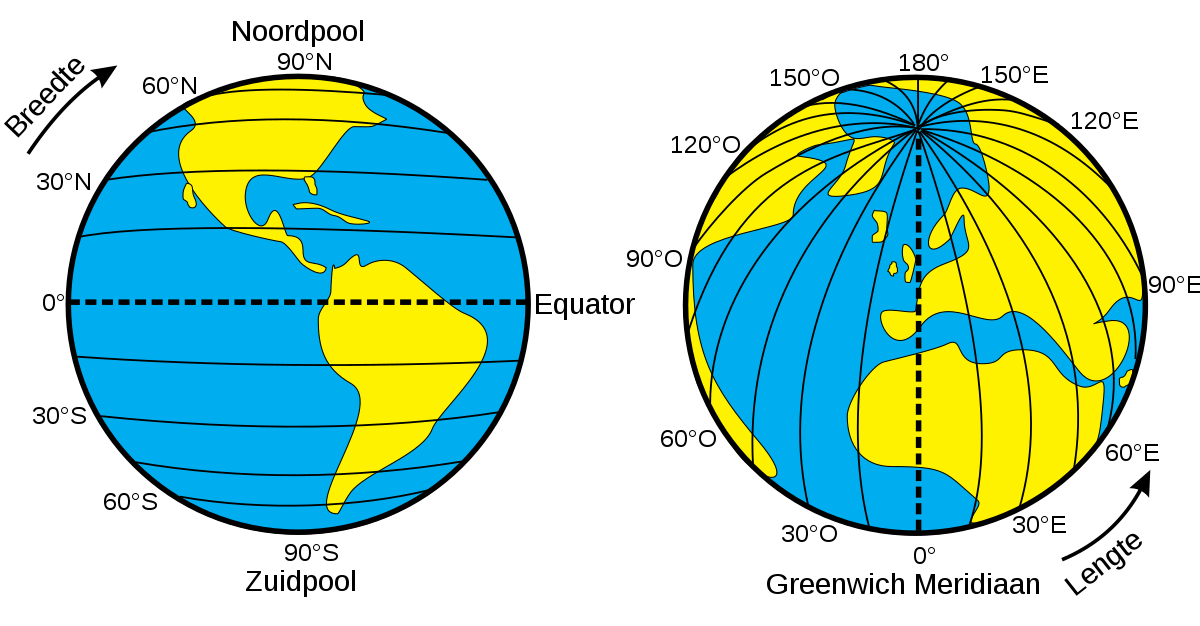
Terwijl de euclidische meetkunde over rechte vlakken en ‘rechte’, isotrope ruimten gaat, betreft de meetkunde van Lobatsjevski en Bolyai hyperbolische oppervlakken en ruimten, waaruit de euclidische meetkunde vanzelf weer tevoorschijn komt als het vijfde postulaat eraan wordt toegevoegd. Met de korte tijd later geformuleerde meetkunde van de bolle of elliptische oppervlakken en ruimten door Bernhard Riemann lag de wiskunde die Einstein nodig had voor zijn vierdimensionale gekromde tijdruimte klaar. In deze meetkunden gaan er door een punt buiten een lijn wel degelijk vele lijnen die er evenwijdig aan lopen – lengtecirkels op het aardoppervlak die vanaf de evenaar evenwijdig naar het noorden lopen gaan allemaal door één punt: de Noordpool – en de som van de hoeken van een driehoek kan allerlei waarden groter en kleiner dan 180 graden aannemen: bekijken we de driehoek op het aardoppervlak gevormd door de Noordpool als top en een stuk van de evenaar als basis, dan is de som van de twee basishoeken alleen al altijd 180 graden, en kan de tophoek nog allerlei verschillende waarden van 0 tot 360 graden aannemen. In de meetkunde van hyperbolische oppervlakken is de som van de hoeken van een driehoek juist altijd kleiner dan 180 graden.

De tweelingparadox

Massa heeft niet alleen een kromming van de ruimte tot gevolg, maar ook een vertraging van de tijd, en hoe meer massa, hoe groter de versnelling of hoe groter de kromming van de ruimte ter plaatse, en hoe trager de tijd verloopt. De redeneringen daarvoor zijn van dezelfde aard als die bij de speciale relativiteitstheorie gebruikt zijn, alleen een stuk ingewikkelder. Van Einsteins hogesnelheidstrein met constante snelheid weten we al dat voor iemand langs de spoorbaan de klokken in de trein langzamer lopen en dat de klok vóór in de trein een andere tijd aanwijst dan die achterin, maar beide klokken lopen tenminste nog wel even snel. Gedurende de periode dat de trein optrekt is ook dit laatste niet meer het geval en loopt de klok achter in de trein langzamer dan die voorin en hoe groter de versnelling hoe groter het verschil in het tempo waarmee de tijd verstrijkt. En omdat dit geen gevolg is van de (relatieve) snelheid maar van de (absolute) versnelling is dit tempoverschil van de tijd niet wederkerig.

Hoewel fysisch niet helemaal correct geeft dit verschijnsel wel enig inzicht in de beruchte tweelingparadox: de door een toevallige genetische mutatie avontuurlijk geworden helft van een eeneiige tweeling heeft besloten astronaut te worden en laat zich met een raket de ruimte inschieten om na enige tientallen jaren om te keren en naar de aarde terug te vliegen.

Als hij door zijn tweelingbroer wordt opgewacht moeten ze tot hun verbazing constateren dat de astronaut een stuk jonger is gebleven dan zijn op aarde achtergebleven broer. Volgens Einsteins vergelijkingen is het horloge van de ruimtereiziger, door de enorme versnellingen die bij het starten, landen en omkeren gedurende zijn tocht zijn opgetreden, langzamer gaan lopen en dit keer betreft het geen wederkerig verschijnsel omdat het hier om versnelling gaat en dit heeft geen relatief, maar een absoluut karakter. Wegens de equivalentie van versnelling en zwaartekracht moet evenzo gelden dat mensen in een sterker zwaartekrachtveld minder snel verouderen dan mensen in een zwakker veld: wie boven op een berg woont leeft korter dan zijn tweelingbroer in het dal, al scheelt het niet meer dan een uiterst kleine fractie van een seconde.

Vanwege de schijnbare absurditeit is de tweelingparadox door twijfelaars wel aangevoerd als doorslaggevend argument tegen de juistheid van de relativiteitstheorie. Maar toen de zeer nauwkeurige cesiumklok eenmaal beschikbaar was, zijn er in 1972 twee daarvan met een vliegtuig rond de aarde gestuurd, waar ze door de versnelling die ze in hun cirkelbaan ondergingen tijd verloren bleken te hebben ten opzichte van de twee identieke klokken die op de grond waren achtergelaten, en het verschil in tijd klopte precies met Einsteins voorspelling. Vanwege de prijs van twee vliegtickets (een voor de onderzoeker en een voor de klokken) is dit een van de goedkoopste cruciale experimenten geweest die er ooit in de geschiedenis van de moderne wetenschap zijn uitgevoerd.^[21]

Er zijn nog wel meer, en veel duurdere experimenten uitgevoerd die Einsteins gelijk hebben bevestigd. Een klassiek niet te verklaren kleine afwijking in de beweging van de planeet Mercurius in het zwaartekrachtveld van de zon – de verplaatsing van het perihelium − blijkt precies te kloppen met de uitkomst van Einsteins berekening, en ook de tijdens een zonsverduistering in 1919 bij het eiland Principe door de Britse astronoom Arthur Eddington gemeten afbuiging die lichtstralen ondergaan als gevolg van de ruimtekromming in de buurt van zware lichamen is in overeenstemming met Einsteins voorspelling. Toen naar aanleiding van het laatste geval Einstein van Arthur Eddington het bericht ontving waarin het succes van zijn theorie werd bevestigd en hem werd gevraagd hoe hij zich gevoeld zou hebben als hij ongelijk had gekregen, schijnt hij gezegd te hebben dat het hem in dat geval zeer zou spijten voor de Lieve Heer, omdat de theorie nu eenmaal juist is. In een later schrijven heeft Einstein deze opmerking toegelicht met het idee dat de kracht van een theorie niet zit in het voorspellende vermogen ervan, maar in de eenvoud, de schoonheid en de logische consistentie.^[22] Maar het is hoe dan ook een fascinerend filosofisch probleem dat een zo abstracte wiskundige theorie zo’n tot in de details juiste beschrijving van de werkelijkheid kan geven.

Dat we in de praktijk geen last zouden hebben en dus ook geen rekening hoeven te houden met de zeer kleine afwijkingen in de tijd die bewegende klokken ondergaan, is tegenwoordig niet meer waar. Voor de plaatsbepaling op aarde worden gps-systemen gebruikt waarbij lichtsignalen tussen satellieten en de aarde heen en weer worden gestuurd. Als gevolg van de beweging en het mindere zwaartekrachtveld op grotere hoogte loopt de klok in de satellieten een heel klein beetje langzamer dan die op aarde en zou er, als daar geen correctie voor wordt aangebracht, geen sprake kunnen zijn van een enigszins nauwkeurige plaatsbepaling.

Ons ‘hier’ en ‘nu’ in het universum

Een wel heel bijzondere consequentie van Einsteins relativiteitstheorie is dat er in het universum geen sprake is van een overal geldig ‘nu’, of met andere woorden: gelijktijdigheid van gebeurtenissen in het universum is een zinloos begrip. Als van de hiervoor al opgevoerde tweeling er eentje, zeg A, naar Mars is gereisd en de andere, zeg B, vraagt zich op aarde af wat zijn broer op dit eigenste moment aan het doen is, blijkt er geen zinnig antwoord mogelijk te zijn. Richt broer B zijn telescoop op Mars, dan ziet hij wat broer A zo’n kwartiertje geleden – de tijd dat het licht er gemiddeld over doet om van Mars de aarde te bereiken − aan het doen was en dat is niet ‘nu’. Maar ook het idee dat A ‘nu’ op Mars doet wat hij een kwartier later zou gaan doen klopt niet, omdat A in zijn tijd in staat zou zijn in dat kwartier met de lichtsnelheid naar de aarde terug te reizen en dan naast broer B zou staan in plaats van op Mars. Het universum beschikt niet over een overal voor iedereen geldig heden, er bestaat geen éénduidig begrip over ‘hetzelfde moment’.^[23] In de woorden van de theoretisch natuurkundige Carlo Rovelli:

Ons heden strekt zich niet uit over het hele universum, het is als een bubbel rondom ons. Tot waar reikt die bubbel? Dat hangt af van de nauwkeurigheid waarmee we de tijd bepalen. Als het nanoseconden zijn strekt het heden zich slechts over een paar meter uit, als het milliseconden zijn over enige kilometers. Wij mensen kunnen ternauwernood tienden van seconden onderscheiden, en we kunnen de hele planeet aarde met het grootste gemak zien als een enkele bubbel waarin we het heden beschouwen als één enkele bubbel, waarin we het heden beschouwen als het moment dat we allemaal gemeenschappelijk hebben. Maar buiten die bubbel gaat dat niet meer op. Daar bevindt zich ons verleden (de gebeurtenissen die hebben plaatsgevonden vóór datgene wat we kunnen zien). En onze toekomst (de gebeurtenissen die zullen plaatsvinden na het moment waarop we, daarvandaan, het hier en nu kunnen zien. Maar tussen eerstgenoemde en laatstgenoemde gebeurtenissen ligt een tijdspanne die verleden nog toekomst is maar wel een duur heeft: vijftien minuten op Mars, acht jaar op Proxima b, miljoenen jaren in de Andromedanevel. Dat is het uitgebreide heden. Wellicht de grootste en vreemdste van Einsteins ontdekkingen.^[24]

Zwarte gaten, wormgaten en de oerknal

Einsteins relativistische vergelijkingen voor de gekromde, vierdimensionale tijdruimte − die in de verte wel iets weg hebben van Maxwells vergelijkingen voor elektromagnetische golven – hebben twee betrekkelijk eenvoudige oplossingen voor extreme gevallen: de eerste leidt tot het bestaan van gelokaliseerde zwarte gaten en de tweede zegt iets over de toestand van het universum als geheel.

Een zwart gat ontstaat als er zo veel massa op een bepaalde plaats is samengebald dat het hemellichaam, een ster bijvoorbeeld, klassiek gesproken onder zijn eigen gewicht bezwijkt en in elkaar stort. De optredende krachten zijn zo groot dat de ruimte tussen de kernen en de omringende elektronen van de atomen waaruit de materie is opgebouwd in elkaar wordt gedrukt, waardoor de negatief geladen elektronen in de uit positief geladen protonen en neutronen bestaande kernen terechtkomen, met de protonen elektrisch neutrale neutronen vormen, zodat een compacte neutronenmassa overblijft. Zou dat met onze planeet gebeuren dan kromp de hele aardbol ineen tot de grootte van een luciferdoosje, waarbij het totale gewicht niet zou veranderen. Gelukkig heeft de aarde daar veel te weinig massa voor en is er minstens zoiets als tienmaal de massa van onze zon voor nodig om eerst een neutronenster en bij nog verdere verdichting een zwart gat te kunnen vormen. De resulterende zwaartekracht van een zwart gat is zo sterk, of de ruimte is zo gekromd, dat het zelfs voor het licht (ook fotonen hebben tenslotte massa, hoe gering ook) niet meer mogelijk is om eruit te ontsnappen, vandaar ook de naam.

Verder is de tijd er, van­wege het enorme zwaartekrachtveld, zo vertraagd dat een seconde er onein­dig lang duurt. Omgekeerd zal voor een (hypothetisch) persoon die zich aan de rand van een zwart gat bevindt, zijn eigen tijd strikt normaal lijken te verstrijken, terwijl de geschiedenis van de rest van het universum in een razend tempo aan hem voorbijtrekt, zoals M. Vasalis dat in het gedicht ‘Tijd’ heeft beschreven:

Ik droomde, dat ik langzaam leefde…
langzamer dan de oudste steen.
Het was verschriklijk: om mij heen
schoot alles op, schokte of beefde
wat stil lijkt.^[25]

Van de fysische wetmatigheden in het zwarte gat, waar de tijd stilstaat en de ruimte oneindig sterk gekromd is, weten we niets en alle verhalen die erover verteld worden – van wormgaten die naar andere universums leiden tot aan kosmisch schuim waarin voortdurend parallelle werelden worden geboren ‒ horen (voorlopig) tot de sciencefiction, maar een beetje fictie in de wetenschap kan op z’n tijd zeker geen kwaad.

Nemen we een lijnstuk in de ‘rechte’ ruimte in gedachten, waarvan het begin- en eindpunt een kosmisch gesproken kippeneindje van één lichtjaar uit elkaar liggen, dan zouden wij met een voor aardse begrippen zeer hoge snelheid van zeg tienduizend kilometer per uur er een beetje afgerond toch nog een miljard jaar over doen om die afstand af te leggen. Vandaar dat Hendrik Casimir onze uitstapjes in de ruimte kon afdoen als planetair bermtoerisme. Maar stel nu eens dat die ruimte zodanig sterk gekromd is dat die twee punten naar elkaar toe worden gebogen en in het extreme geval naast elkaar komen te liggen, dan zou het nog maar één stap door een wormgat vergen om de afstand te overbruggen, en waren we in die ene stap van planetaire bermtoeristen tot volwaardige reizigers in de tijdruimte geworden. De astronoom David Darling geeft toe dat onze natuurkunde weliswaar nog lang niet in staat is ons met zo’n huzarenstukje van de aarde over te brengen naar een andere leefbare omgeving in ons eigen of in een ander universum, maar dat we om dat voor elkaar te krijgen nog wel een paar honderd miljard jaar de tijd hebben voor ons heelal zal zijn afgetakeld.^[26] ‘Nou Darling’, zouden we daarop terug kunnen zeggen, ‘vanuit wetenschappelijk perspectief hebben we misschien nog wel miljarden jaren de tijd, maar vanuit ethisch oogpunt moeten we eerst nog maar eens zien de komende eeuw fatsoenlijk door te komen (zie hoofdstuk II).’

De tweede eenvoudige oplossing van Einsteins vergelijkingen is mogelijk omdat het universum zo groot is dat de verdeling van de massa over de ruimte als homogeen kan worden beschouwd. De verrassing die deze oplossing oplevert is dat het universum niet in statisch evenwicht kan verkeren: het moet of uitdijen of inkrimpen. Einstein was daar zo door uit het veld geslagen dat hij ter correctie een zogenaamde ‘kosmologische term’ in de formules heeft ingevoerd om zo een evenwichtstoestand te forceren. Maar later, toen de Amerikaanse astronoom Edwin Hubble in 1927 had aangetoond dat het universum inderdaad in beweging is en expandeert, noemde Einstein zijn aanname de grootste fout in zijn leven.^[27]

Hubble bepaalde de uitdijing van het heelal door meting van de golflengte van het licht dat door sterrenstelsels in de omgeving van onze eigen Melkweg wordt uitgezonden. Als een lichtbron van ons weg beweegt, verschuift de golflengte van het licht naar de rode kant van het spectrum – het dopplereffect – en de verschuiving wordt evenredig groter met het toenemen van de snelheid.

De metingen van Hubble leverden drie bijzondere resultaten op: ten eerste dijt het heelal uit, ten tweede bewegen alle sterrenstelsels van ons af, en ten derde bewegen ze sneller van ons af naarmate ze verder weg staan. Dat alle sterrenstelsels van ons af bewegen betekent niet dat wij ons ook in het centrum van het heelal bevinden. Om duidelijk te maken wat er wel aan de hand is moeten we weer even terug naar het ballonoppervlak: de tweedimensionale, in de derde dimensie gekromde wereld van de Platlanders. Als we op de ballon regelmatig over het oppervlak verdeelde stippen aanbrengen waarmee we de sterrenstelsels in die tweedimensionale ruimte aangeven, en we blazen de ballon vervolgens op, dan zien we dat alle stippen van elkaar weg bewegen, op welke stip we ons zelf ook bevinden, en ook bewegen de stippen op tweemaal zo grote afstand tweemaal zo snel weg. En we zien ook dat het niet de stippen zijn die over het boloppervlak bewegen, maar het is het oppervlak zelf dat uitdijt. Er bevindt zich dus geen speciaal punt op het ballonoppervlak dat zich als ‘centrum’ van alle andere punten onderscheidt: geen enkel punt is centrum of alle punten zijn het. Het ‘echte’ centrum van de uitdijing bevindt zich buiten het tweedimensionale oppervlak in het midden van de driedimensionale ballon. Vertalen we dat naar een dimensie hoger dan geldt ook voor onze driedimensionale ruimte dat het centrum van uitdijen zich niet daarin bevindt, maar daarbuiten in het centrum van de voor ons niet voorstelbare vierdimensionale tijdruimte. En het zijn ook niet de sterrenstelsels die in de ruimte uit elkaar bewegen, maar het is de ruimte zelf die uitdijt, waarbij de sterrenstelsels gewoon op hun plaats in de ruimte kunnen blijven.

Gaan we nog een stap verder dan kunnen we ons afvragen wat er in het verleden gebeurd moet zijn waardoor we in de huidige situatie terecht zijn gekomen. Daarvoor hoeven we de pijl van de tijd en daarmee de uitdijing van het heelal maar om te draaien, en dan zien we onze leeglopende vierdimensionale tijdruimteballon zich ongeveer 13,8 miljard jaar geleden in één punt samentrekken en verdwijnen. Misschien zal dat in de zeer verre toekomst − als de uitdijing eerst is vertraagd, vervolgens tot stilstand is gekomen en ten slotte is overgegaan tot inkrimping − ook wel gebeuren: de Big Crunch. Voor de ‘omvang’ van ons universum geldt dat de straal daarvan 13,8 miljard lichtjaar zou bedragen, als de ruimte in die tijd ook niet nog snel zou zijn uitgedijd, en daardoor intussen 46 miljard lichtjaar bedraagt. Dat betreft dan alleen maar de voor ons zichtbare ruimte: het licht van de sterren die sneller van ons weg bewegen dan de lichtsnelheid zal ons niet kunnen bereiken – nu niet en nooit niet – en valt buiten onze waarnemingshorizon, wat betekent dat we de ‘echte’ diameter van ons universum nooit zullen kunnen kennen, noch het aantal daarin aanwezige sterren. Maar mogelijk is dat te ver gezocht, omdat de ruimte ‒ net als het ballonoppervlak ‒ niet oneindig groot is maar in zichzelf besloten kan zijn en er ‒ net als de punten op het ballonoppervlak ‒ slechts een eindig aantal sterrenstelsels in past.

Los van de wiskunde die aan dit alles ten grondslag ligt en die alleen door de echte specialisten kan worden begrepen, is het totaalbeeld dat er van ons universum uit tevoorschijn komt alleszins overzichtelijk. Tenminste, dat zou het zijn als er niet een paar onbegrepen verschijnselen waren die zich maar niet willen laten inpassen, zoals dat ook aan het eind van de negentiende eeuw het geval was. Zo zijn er wat problemen met de simpele slinger die zich tijdens zonsverduisteringen maar niet aan de bekende mechanische wetten wil houden, en gedragen ruimtesondes aan de rand van ons zonnestelsel zich af en toe of er een nog onbekende kracht aan het werk is.^[28] Ook is maar niet helder te krijgen wat zich allemaal in ons universum moet bevinden om alle verschijnselen te kunnen verklaren. Eigenlijk is maar van vier procent bekend dat het uit gewone materie bestaat, en dan voornamelijk uit waterstof en helium. De onbekende rest wordt aangeduid met donkere materie (23 procent) omdat die er wel moet zijn maar niet is te zien, en de tegenhanger daarvan (73 procent), die om in de stijl te blijven donkere energie wordt genoemd.^[29] Als de overeenkomst met het eind van de negentiende eeuw nog verder mag worden doorgetrokken, dan is ook nu het wachten op de revolutionaire doorbraak die alle bestaande theorieën weer op losse schroeven zal zetten, maar die aanvankelijk door niemand zal worden geloofd.

Hoe verder weg de objecten in het uitdijende universum staan, hoe ‘ouder’ ze zijn en hoe uitgestrekter hun ‘nu’. Dat betekent dat de oudste, miljarden lichtjaren verwijderde sterren en nevels vanuit ons standpunt een ‘nu’ hebben dat zich ook over miljarden jaren uitstrekt. Maar we menen ook te weten dat het universum bij gelegenheid van de oerknal 13,8 miljard jaar geleden is ontstaan, wat zich moeilijk laat rijmen met het ontbreken van een goed gedefinieerd nu in de tijdstroom. Reden voor sommige kosmologen om aan Einsteins relativistische tijd te gaan twijfelen en weer in een absolute tijd te geloven.^[30] En Einstein zelf vond zijn theorieën over de tijd weliswaar beter dan die van Aristoteles en Newton, maar twijfelde er geen moment aan dat hij er niet het laatste woord over had gezegd. In 1949 schreef hij in een brief aan een vriend:

Jij denkt dat ik met tevredenheid op mijn levenswerk terugkijk, maar bij nadere beschouwing gaat het om iets heel anders. Van geen enkel begrip ben ik overtuigd dat het zal standhouden, en ik twijfel eraan of ik überhaupt op de juiste weg ben.^[31]

1. Vincent Icke, Niks relatief; de speciale relativiteitstheorie zonder formules, Contact 2005, blz. 40. ↑

2. Robert March, Physics for Poets, McGraw-Hill 1978, blz. 108. ↑

3. Martijn van Calmthout, Einsteins licht; een leven met relativiteit, Contact 2005, blz. 50-52. ↑

4. Robert March, Physics for Poets, McGraw-Hill 1978, blz. 111. ↑

5. Rogi Wieg, ‘Dagboek van een bloem, in: Het boek van de beminnelijkheid, De Arbeiderspers 2000, blz. 49. ↑

6. Hendrik Lorentz, uit: David Darling, Zwaartekracht. Van Aristoteles tot Einstein en verder, (vert. Eddy Echternach), Veen 2006, blz. 141. ↑

7. Erhard Scheibe, Die Philosophie der Physiker, C.H. Beck 2006, blz. 196. ↑

8. Max Planck, uit: David Darling, Zwaartekracht. Van Aristoteles tot Einstein en verder, (vert. Eddy Echternach), Veen 2006, blz. 152. ↑

9. Rogi Wieg, ‘Dagboek van een bloem’, in: Het boek van de beminnelijkheid, De Arbeiderspers 2000, blz. 49. ↑

10. A.F.Th. van der Heijden, Weerborstels, CPNB 1992, blz. 71-72. ↑

11. A.F.Th. van der Heijden, Weerborstels, CPNB 1992, blz. 73. ↑

12. Carlo Rovelli, Het mysterie van de tijd, (vert. Yond Boeke en Patty Krone), Prometheus 2018, blz. 15. ↑

13. Edwin Abbott Abbott, Flatland, 1844. ↑

14. Lucretius, uit: Timothy Ferris, Ruimte en tijd; verkenningen rond de Melkweg, (vert. George Beekman, Aaldert v. d. Bo­gaard, Govert Schilling), De Haan 1990, blz. 191. ↑

15. Martijn van Calmthout, Einsteins licht; een leven met relativiteit, Contact 2005, blz. 116. ↑

16. Martijn van Calmthout, Einsteins licht; een leven met relativiteit, Contact 2005, blz. 117. ↑

17. Martijn van Calmthout, Einsteins licht; een leven met relativiteit, Contact 2005, blz. 119-120. ↑

18. Jan Hilgevoord, Ruimte, tijd en relativiteit; van Euclides tot Einstein, Studium Generale Universiteit Utrecht, 2000. ↑

19. Uit: Timothy Ferris, Ruimte en tijd; verkenningen rond de Melkweg, (vert. George Beekman, Aaldert van de Bo­gaard, Govert Schilling), De Haan 1990, blz. 190. ↑

20. David Darling, Zwaartekracht. Van Aristoteles tot Einstein en verder, (vert. Eddy Echternach), Veen 2006, blz. 146-147. ↑

21. Robert March, Physics for Poets, McGraw-Hill 1978, blz. 124-125. ↑

22. Erhard Scheibe, Die Philosophie der Physiker, C.H. Beck 2006, blz. 137. ↑

23. Carlo Rovelli, Het mysterie van de tijd, (vert. Yond Boeke en Patty Krone), Prometheus 2018., blz. 36-37 ↑

24. Carlo Rovelli, Het mysterie van de tijd, (vert. Yond Boeke en Patty Krone), Prometheus 2018, blz. 36. ↑

25. M. Vasalis, ‘Tijd’, Uit: Parken en Woestijnen, 1940. ↑

26. David Darling, Zwaartekracht. Van Aristoteles tot Einstein en verder, (vert. Eddy Echternach), Veen 2006, blz. 237. ↑

27. Robert March, Physics for Poets, McGraw-Hill 1978, blz. 149. ↑

28. David Darling, Zwaartekracht. Van Aristoteles tot Einstein en verder, (vert. Eddy Echternach), Veen 2006, blz. 187 e.v. ↑

29. David Darling, Zwaartekracht. Van Aristoteles tot Einstein en verder, (vert. Eddy Echternach), Veen 2006, blz. 209. ↑

30. Grit Kalies, Raumzeit, Mitteldeutscher Verlag 2019, blz. 64. ↑

31. Grit Kalies, Raumzeit, Mitteldeutscher Verlag 2019, blz. 137. ↑