– DE MODERNE NATUURKUNDIGE THEORIEËN –

1. Van determinisme naar chaostheorie – 2. Van determinisme naar kwantumtheorie –
3. Ruimte, tijd en relativiteit

Voorspellen is bijzonder moeilijk, vooral de toekomst.
(Toegeschreven aan onder anderen: Woody Allen, Niels Bohr, Winston Churchill, Confucius, Wim Kan, Groucho Marx, Gerard Reve, Mark Twain en Oscar Wilde)^[1]

Van determinisme naar chaostheorie

In 1687 formuleerde de in literatuur en andere kunsten nauwelijks geïnteresseerde wis- en natuurkundige Isaac Newton in zijn Principia definitief de wetten en axioma’s van de klassieke mechanica.

Deze vormden, na de tweeduizendjarige hegemonie van het aristotelische wereldbeeld, op hun beurt meer dan tweehonderd jaar lang het onbetwijfelbare fundament van de natuurkunde van hemel en aarde − en daarmee van het hele wetenschappelijke wereldbeeld. Hoewel daar onmiddellijk aan moet worden toegevoegd dat de Arabische denker Avicenna er al zeshonderd jaar vóór Newton blijk van heeft gegeven begrepen te hebben dat een voorwerp op dezelfde plaats blijft, of zich met constante snelheid in een rechte lijn blijft voortbewegen, tenzij er een kracht op wordt uitgeoefend, wat toch opmerkelijk mag heten.^[2] Maar zoals als vaker gezegd verlangt een goed idee om algemeen ingang te kunnen vinden kennelijk meer dan alleen het goede idee zelf.

In Newtons wereldbeeld wordt het universum opgevat als een door superingenieur God in elkaar gezet mechanisch systeem, als een gigantisch uurwerk. Planeten, manen, sterren en kometen vliegen even voorspelbaar door de ruimte als biljartballen over het groene laken, en uit de behoudswetten voor materie en energie volgt dat oorzaken altijd even grote gevolgen moeten hebben: door op de grond te stampen krijgen we de aarde niet uit haar baan, en een vlinder kan uiteraard geen boom ontwortelen. In het vervolg gesteund door de opvatting van de Britse empiristen Thomas Hobbes, John Locke en David Hume, vond men dat het beeld van een mechanisch heelal niet alleen van toepassing moest zijn op de materiële wereld, maar ook op allerlei andere gebieden die tegenwoordig tot de sociale en geesteswetenschappen worden gerekend. Al in 1691 verscheen in Engeland het boek Political Arithmetic, waarin de auteur Sir William Petty in het voorwoord schrijft dat hij zich uitsluitend zal uitdrukken in termen van getal, gewicht en maat, en geeft dan als voorbeeld dat Frankrijk, hoewel er dertien keer zo veel mensen wonen als in Holland en Zeeland, en het tachtig keer zo veel bruikbaar land bevat, toch niet dertien keer rijker en sterker is en al helemaal niet tachtig keer, maar hooguit drie keer.^[3] En in 1728, een jaar na Newtons dood, publiceerde Jean-Théophile Desaguliers het boek The Newtonian System of the World: The Best Model of Government, an Allegorial Plan, waarin ook hij de newtoniaanse wetmatigheid toepast op de politiek.

Men was ervan overtuigd dat Newtons wetten de mogelijkheid inhouden om de loop van de hele kosmische machinerie zowel naar een ver verleden terug te rekenen als naar een verre toekomst te voorspellen. In 1812, één en een kwart eeuw na het verschijnen van de Principia, was dat voor de Franse wiskundige en Napoleons hofastronoom Pierre Simon de Laplace de aanleiding tot het schrijven van zijn beroemde passage over de in essentie volledige en exacte bepaaldheid van heden, verleden en toekomst van de wereld, al zijn bewoners en hun avonturen:

Een denkende geest die op een bepaald moment alle natuurwetten en tevens de toestand van alle dingen waaruit de wereld bestaat zou kennen, zou als hij intelligent genoeg was om deze gegevens te analyseren, zowel het verleden als de toekomst helder voor ogen zien.^[4]

Toen zijn zeer godvruchtige werkgever Napoleon Bonaparte bij hem informeerde waar in dat wereldbeeld de plaats van God dan wel mocht zijn, antwoordde Laplace dat hij die hypothese niet meer nodig had.

De invloed van Laplaces werk was, ondanks het onverhulde atheïsme, ongekend groot. Toen Klemens von Metternich in het begin van de negentiende eeuw door Europa reisde om het politieke machtsevenwicht tot stand te brengen, had hij een exemplaar van het werk van Laplace in zijn bagage, en ook de opstellers van de Amerikaanse grondwet maakten er gebruik van bij het ontwerpen van een regeermachine waarvan de rechten en plichten van de burgers in elkaar zouden passen als de onderdelen van een uurwerk. En de succesvolle uitbreiding van de industriële beschaving, met haar reusachtige ratelende machines, haar verbluffende technische hoogstandjes, haar opkomst van de spoorwegen en al haar nieuwe industrietakken zoals staal-, textiel- en auto-industrie, leek dit beeld van de wereld als de meccanodoos van een goddelijke uitvinder alleen maar te bevestigen.^[5]

Ook Verlichtingsdenkers als Voltaire en Georg Christoph Lichtenberg deden met overtuiging een duit in het mechanistische zakje, waarbij ze beiden schijnbaar toevallig het zo verraderlijk onvoorspelbare weer op het oog hadden.

Voltaire schreef onder het lemma ‘Lot’ in zijn Filosofische woordenboek dat een boer denkt dat de hagel toevallig op zijn akker is terechtgekomen, maar dat een filosoof weet dat toeval niet be­staat en dat het, in de wereld zoals die is geordend, niet mogelijk is dat de hagel ergens anders terechtkomt dan juist op die plek.^[6] En Lichtenberg was niet minder stellig met zijn bewering dat het ‘object van de meteorologie’ niets anders is dan een machine waarvan het aandrijfmechanisme mettertijd steeds beter begrepen zal worden. Er zit heus geen vrij wezen achter onze weersveranderingen, schreef Lichtenberg, geen eigengereide, jaloerse en verliefde creatuur, die om zijn geliefde te plezieren midden in de winter de zon weer in het teken van de kreeft laat staan.^[7]

Bij al deze wiskunde en mechanica in het wereldbeeld mag zeker niet vergeten worden dat het hierbij niet gaat om een typisch zeventiende- of achttiende-eeuwse opvatting, maar dat Plato tweeduizend jaar eerder al een geheel gemathematiseerd beeld van de menselijke samenleving voor ogen stond, waarover George Sarton schrijft dat het geheim van de kosmos of het universum in de Griekse Oudheid berustte op orde en maat. Plato breidde dat concept uit naar alle economische en politieke verschijnselen, en hij deed dat zonder enige terughoudendheid. In de perfecte, als een machine functionerende stadstaat moet alles geregeld zijn en niets aan het toeval worden overgelaten, zodat er geen keuzemogelijkheden zijn en geen ruimte voor verbeelding. Sommige hoofdstukken in De wetten reguleren het privéleven zo gedetailleerd en onbeperkt dat ze de moderne geest zelfs weerzinwekkend en obsceen voorkomen. Plato argumenteert soms met woorden alsof het meetkundige symbolen zijn, en in dat opzicht mag hij beschouwd worden als de vroegste voorloper van de symbolische of wiskundige logici van vandaag.^[8] Wordt de Verlichting tegenwoordig bij voorkeur gezien als een zich definitief ontworstelen aan de tweeduizendjarige autoriteit van Aristoteles – met als overtuigend voorbeeld Spinoza’s op de meetkunde gebaseerde Ethica − dan moeten we daar nu als kanttekening bijzetten dat het ook als een inruilen van Aristoteles’ ideeën voor die van de nog wat oudere Plato kan worden begrepen.

Maar hoe dan ook, zo’n alomvattend logisch en mechanistisch wereldbeeld, zonder spannende verrassingen en uitdagende keuzemogelijkheden, is ongeveer het saaist denkbare en het valt dus alleszins te begrijpen dat dit niet lekker lag (en ligt) bij Arthur Schopenhauer en andere aanhangers van het romantische wereldbeeld, bij wie het gevoel en de kunst de prioriteit genieten boven de strikte orde van de rede en de wetenschap:

En zo zou ten slotte de hele wereld, met alle dingen die er deel van uitmaken, slechts een mechanisch kunststuk zijn zoals het door hefbomen, raderen en zand aangedreven speelgoed dat een mijn of een boerderij moet verbeelden.’^[9]

Maar in het jaar 1846, nog tijdens Schopenhauers leven, scheen het strikt deterministische wereldbeeld van Newton door de Franse astronoom Urbain Leverrier toch op spectaculaire wijze te worden bevestigd. Van de zeven toen bekende planeten vertoonde de baan van de buitenste, Uranus, een geringe afwijking van wat er volgens de voorspelling werd verwacht. Door gebruik te maken van Newtons wetten slaagde Leverrier erin, na eindeloos en ingewikkeld rekenwerk, die afwijking te verklaren door het bestaan van een achtste planeet aan te nemen en ook de baan en op ieder moment de positie ervan te bepalen. Op 23 september ontving de Berlijnse sterrenwacht de uitkomst van Leverriers berekening en gebeurde het allermooiste wat een theorie zich maar kan wensen: diezelfde nacht nog werd de onbekende planeet Neptunus vrijwel exact op de voorspelde plaats waargenomen. Het succes voor Newtons mechanica zou blijvend ongekend groot zijn geweest, als later niet was gebleken dat Leverrier een onjuiste vereenvoudiging in zijn berekeningen had aangebracht. Dat de planeet toch op de door hem berekende plaats werd aangetroffen was een grote toevalligheid: zo’n planeet moet toch érgens staan.^[10] Vermeldenswaard is verder nog dat het bestaan van Neptunus, door de afwijking in de baan van de in 1781 door William Herschel ontdekte planeet Uranus, tegelijk met Leverrier door de Engelse astronoom John Adams werd voorspeld, zonder dat ze van elkaars werk wisten, en dat Neptunus al meermalen eerder was waargenomen, onder anderen door Galilei, zonder als nieuwe planeet te zijn herkend.

Na ruim twee eeuwen absolute heerschappij kregen Newtons onwrikbaar geachte wetmatigheden het rond de eeuwwende 1900 in het huis van de natuurkunde binnenskamers serieus aan de stok met maar liefst vier revolutionaire wetenschappelijke ideeën tegelijk: de chaostheorie, de thermodynamica of warmteleer, de kwantumtheorie en de beide relativiteitstheorieën. Opvallend daarbij is dat, hoewel alle vier de theorieën Newtons systeem aanzienlijk verbeteren op de deelgebieden van het niet-lineaire, het statistische, het hele kleine en het hele snelle, ze elkaar onderling slecht verdragen. Pogingen om ze onder één hoedje te vangen zijn óf speculatief óf hebben het geforceerde karakter van een gedwongen huwelijk. De kwantumtheorie en de speciale relativiteitstheorie, waaraan in eerste instantie de namen van Max Planck en Albert Einstein zijn verbonden, dateren van respectievelijk 1900 en 1905, terwijl Ludwig Boltzmann al aan het eind van de negentiende eeuw de basis legde voor de statistische thermodynamica en te zelfder tijd ook de kern van de chaostheorie werd blootgelegd door onder anderen de Franse wiskundige Henri Poincaré.

De chaostheorie

Poincarré bewees in het winnende essay van een door de Zweedse koning Oscar II uitgeschreven prijsvraag, dat het voor een betrekkelijk eenvoudig mechanisch probleem − de wisselwerking tussen drie voorwerpen, zoals de zon, de aarde en de maan − tegen zijn eigen verwachtingen in niet mogelijk is een exacte oplossing te vinden van de wiskundige vergelijking die het systeem beschrijft. Bij berekeningen kunnen kleine variaties in de gekozen beginsituatie grote afwijkingen in het toekomstige gedrag van dat systeem tot gevolg hebben, wat de voorspelbaarheid op enige termijn uiteraard niet ten goede komt en wij kunnen denken met een toevallig verschijnsel van doen te hebben.^[11]

Maar ook met zijn inzichten in gecompliceerde systemen die we tegenwoordig typisch chaotisch noemen was Poincaré zijn tijd ver vooruit, gezien zijn beschouwing over de weerkunde:

Waarom hebben meteorologen zoveel moeite om het weer ook maar enigszins nauwkeurig te voorspellen? Waarom lijken regenbuien en stormen per toeval te komen, zodat veel mensen het heel gewoon vinden te bidden voor regen of mooi weer, terwijl ze het belachelijk zouden vinden in hun gebed om een zonsverduistering te vragen? We zien dat grote storingen zich meestal voordoen in streken waar de atmosfeer in labiel evenwicht is en dat er een cycloon zal ontstaan, maar waar precies? Dat kunnen ze niet voorspellen: een tiende graad meer of minder op een bepaald punt en de cycloon breekt hier en niet daar uit, hij richt zijn ravage aan in een streek die hij anders gespaard zou hebben. Mits kennis van dat tiende van een graad, had men die plaats kunnen voorspellen, maar de waarnemingen waren niet talrijk of nauwkeurig genoeg, en daarom lijkt alles een kwestie van toeval.^[12]

Met zijn bewering dat meer en nauwkeuriger waarnemingen de weersvoorspelling tot in een verre toekomst veel preciezer en betrouwbaarder zouden kunnen maken had Poincaré het weliswaar bij het verkeerde eind ‒ een honderdste graad meer of minder maakt de weersvoorspelling op wat langere termijn even onbetrouwbaar ‒ maar in principe zat hij met zijn ideeën over onvoorspelbaarheid op het juiste spoor.

Dat de chaostheorie in de eerste decennia na 1900 niet zo voorspoedig van de grond kwam als de andere nieuwe theorieën is te wijten aan het onvermogen van Poincaré zijn collega’s te overtuigen van het belang van chaotische verschijnselen die toen behalve als moeilijk vooral als uiterst vervelend werden beschouwd, vanwege het vele tijdrovende rekenwerk dat er voor nodig is. Daarvoor moest eerst de rekenkracht van de elektronische computer nog ter beschikking komen en was het dus even wachten tot na de Tweede Wereldoorlog. Tegenwoordig kan het rekenwerk van de chaostheorie met machtige machines worden aangepakt en ondanks de kinderschoenen waarin de theorie nog staat, kan er wel reeds gesproken worden van een revolutionaire of paradigmatische verandering in het wetenschappelijke denken, vergelijkbaar met die van de andere drie revolutionaire theorieën. In een interview naar aanleiding van het verschijnen van zijn roman Brazzaville strand zei de in Afrika geboren Schotse schrijver William Boyd dat wat hem erg aantrekt in de recente ontwikkelingen in de wis- en natuurkunde dat wetenschappers voor het eerst zijn gaan beseffen dat het oude newtoniaanse beeld van de wereld als een enorme machine die ze op een dag helemaal zullen begrijpen achterhaald is.

Hedendaagse wetenschappers geven grif toe dat ambiguïteit, gebrek aan precisie en toeval allemaal een belangrijke rol spelen:

Dat vind ik erg geruststellend, want het klopt uitstekend met onze eigen ervaring van de wereld. We weten niet eens wat ons de komende vijf minuten zal overkomen, laat staan de komende vijf jaar.^[13]

In Brazzaville strand beschrijft Boyd het chaotisch functioneren van de menselijke geest in het algemeen en die van zijn protagonist Hope in het bijzonder

Mijn haar moet geknipt… De honden zijn weer terug op het strand… Water is een verbinding van twee gassen… Ik moet eigenlijk een nieuwe koelkast kopen… Er is niets in het evolutiedenken waarmee de menselijke geest kan worden verklaard… Günther heeft me gevraagd om hem in München op te zoeken… Hopes hoofd zit vol van dat soort aanflitsende, losse ideeën en waarnemingen terwijl ze met een koud biertje op haar terras zit en naar het ondergaan van de zon kijkt.^[14]

Hopes gedachten tuimelen over elkaar heen en de geringste aanleiding is voldoende om de turbulente stroom een heel andere kant op te sturen. De keuze voor deze beeldspraak is niet toevallig: ook turbulente verschijnselen als stromend water en windvlagen of aan de lijn wapperend wasgoed vertonen een dergelijk chaotisch gedrag, dat ook de voorspellingen van wetenschappelijke beschrijvingen ongewis maakt.

In de openingsalinea van een bundel wetenschappelijke artikelen over de chaostheorie wordt het dagelijkse leven op een vergelijkbare manier beschreven. De auteur schrijft dat we ons er allemaal van bewust zijn dat kleine gebeurtenissen de loop van de geschiedenis ingrijpend kunnen wijzigen: de kogel van een moordenaar die een wereldoorlog kan ontketenen, een toevallige ontmoeting met een onbekende op een feestje, het impulsieve besluit in een vliegtuig te stappen dat voorbestemd blijkt te verongelukken, gebeurtenissen waar romans en verhalen vol mee staan. We verwachten niet anders dan dat ons levenspad ingewikkeld en onzeker is, bezaaid met willekeurige gebeurtenissen die de toekomst onmogelijk te voorspellen maken, reden waarom zo veel mensen de exacte voorspelbaarheid van de wetenschap onbevredigend vinden en moeilijk te rijmen met hun eigen ervaringen in het leven.^[15]

Zowel Boyds roman als de wetenschappelijke tekstbundel heeft de onzekerheden en de onvoorspelbaarheden van de chaostheorie als rode draad en het heeft er alle schijn van dat de literatuur en de wetenschap op dit gebied goed met elkaar overweg kunnen. Een vergelijkbare eensgezindheid in de belangstelling van beide culturen is sinds hun ontstaan in de geschiedenis nauwelijks te vinden. Waar Voltaire en Lichtenberg nog aan twijfelden, maar wat Poincaré al wel vermoedde, is dat het weer een goed voorbeeld is van een natuurkundig systeem dat zich bevindt in het spanningsveld tussen wetenschappelijke voorspelbaarheid en de onzekerheid van een chaotische toekomst vol ‒ soms onaangename ‒ verrassingen. Ondanks de hoge vlucht van de technologie − de waarnemingen van meer dan tienduizend weerstations, schepen, satellieten, ballonnen en vliegtuigen worden doorgeseind naar een enorme computer die met uiterst gedetailleerde modellen de weersontwikkeling van een etmaal in twintig minuten kan doorrekenen^[16] − komt het toch geregeld voor dat de weerkundigen met hun voorspellingen voor de volgende paar dagen de plank behoorlijk misslaan. En aan een voorspelling van langer dan vijf dagen zal niemand zich wagen, zonder er bij te vermelden de hand er niet voor in het vuur te durven steken: de aanvankelijke curve die bij voorbeeld de verwachte temperatuur voor de komende dagen aangeeft, verandert in een steeds breder uitwaaierende pluim. Hoewel Poincaré nog dacht dat met meer gegevens, betere rekenmachines en verfijndere modellen de voorspellende kracht van de meteorologie aanzienlijk zou toenemen, blijkt uit de recente wiskundige ontwikkelingen op het gebied van de chaostheorie dat er aan het voorspellen een fundamentele grens is gesteld. Wat het weer betreft is er sprake van een voorspelbaarheidshorizon van vijf tot zeven dagen waar ook de grootste computer, voorzien van de betrouwbaarste gegevens, niet overheen kan kijken. Wat er achter die horizon ligt blijft principieel voor ons verborgen, en zijn we al met al niet zo heel veel opgeschoten sinds de zeevarende, en daarom zeer in het weer geïnteresseerde Mileziërs, die tweeënhalf duizend jaar geleden donder en bliksem verklaarden als de verwoede bevrijdingspogingen van de wind die door de wolken gevangen wordt gehouden.

Het is daarom te begrijpen dat de huidige belangstelling voor de chaostheorie voor een aanzienlijk deel door de weerkunde wordt gevoed. De meteoroloog Edward Lorenz introduceerde begin jaren zestig een wiskundig model voor het weer dat ondanks de betrekkelijke eenvoud tot zijn verrassing chaotisch gedrag bleek te vertonen.

Over dit voorval vertelt Lorenz dat hij tijdens een van zijn berekeningen besloot om een bepaalde uitkomst gedetailleerder te onderzoeken. Daarvoor koos hij een paar tussentijdse toestanden die door de computer waren uitgeprint, en voerde die weer in als nieuwe beginvoorwaarden voor de verdere ontwikkelingen. Nadat de computer een paar uur later ongeveer twee maanden ‘weer’ had gesimuleerd, bleek er een groot verschil te bestaan met de eerdere uitkomst. Nadat eerst de mogelijkheid van – regelmatig voorkomende – computerpanne was uitgesloten, drong het opeens tot hem door dat de twee uitkomsten niet van dezelfde begintoestanden afkomstig waren. De eerdere berekeningen waren in de computer uitgevoerd tot op zes decimalen nauwkeurig, maar de uitgeprinte resultaten hadden er maar drie, zodat de nieuw ingevoerde beginvoorwaarden door het afronden – wat betekent dat de computer de drie cijfers na het derde decimaal als nullen ziet − lichtelijk afweken van de oude voorwaarden. Deze afwijkingen werden in de loop van de berekeningen exponentieel uitvergroot, wat wil zeggen dat ze verdubbelden in vier gesimuleerde dagen, zodat na twee maanden de uitkomsten niets meer met elkaar gemeen hadden.^[17]

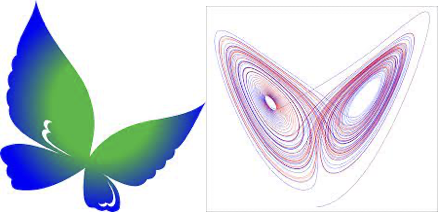
Het ontstaan van chaos in een wiskundig strikt bepaald systeem, waarin elke stap precies is voorgeschreven en er ook geen aanwijsbare verstoringen zijn, lijkt paradoxaal, maar de ervaring van Lorenz laat zien dat er een goede verklaring voor is. Het blijkt dat er ‒ ook betrekkelijk eenvoudige ‒ systemen bestaan waarvan de ontwikkeling in de tijd zeer gevoelig is voor kleine verschillen in de begintoestand. Dergelijke systemen worden door wiskundigen ‘niet-lineair’ en door natuurkundigen ‘ver-uit-evenwicht’ genoemd, omdat oorzaak en gevolg niet van vergelijkbare grootte hoeven te zijn, zo’n beetje als in de Bijbelse uitspraak: wie wind zaait, zal storm oogsten.^[18] Komt zo’n ver-uit-evenwicht-systeem eenmaal in beweging, dan ontwikkelt dit zich niet lineair vanuit de begintoestand, maar breekt resoluut met het verleden en gaat op weg naar een buiten het oorspronkelijke systeem liggende nieuwe toestand, die daarom vreemde aantrekker wordt genoemd. Dat betekent dat aanvankelijk onmerkbaar kleine verschillen in de loop van de berekende ontwikkelingen dramatisch kunnen worden uitvergroot tot complete catastrofes. Die kleine verschillen zitten niet in de onvolledigheid of de onnauwkeurigheid van het model, maar worden veroorzaakt door de rekenaar zelf: ook bij de machtigste computer en het meest gedetailleerde wiskundige model moeten de getallen bij het invullen na een aantal cijfers achter de komma noodzakelijkerwijs worden afgerond. Het weglaten van de rest, wat neerkomt op het verwaarlozen van de speling van nul tot negen in de daarop volgende decimaal, is voldoende om na enige tijd grote verschillen in de einduitkom­sten te veroorzaken. Wat de mogelijke einduitkomsten kunnen zijn valt precies aan te geven, maar dat zijn er zeer vele en ook zeer verschillende, en welke daarvan in werkelijkheid zal worden gerealiseerd is niet te voorspellen. Dit verschijnsel noemde Lorenz om twee redenen het vlindereffect: het bij de berekeningen op geen enkele manier te verdisconteren gefladder van een paar vlindervleugels op de ene plaats in de wereld, kan ertoe leiden dat de ontwikkeling van het weer een verrassende weg inslaat en er enige tijd later ergens anders een tropische orkaan ontstaat die moeiteloos woudreuzen velt, waarbij bovendien de vreemde aantrekker van Lorenz’ systeem de grafische vorm van een vlinder heeft, wat het beestje als naamgever de voorkeur deed krijgen boven de ook wel genoemde vleugelslagen van de zeemeeuw of de sprinkhaan.^[19]

Zelfs als het wiskundige model de weersontwikkelingen exact zou beschrijven, dan nog zou het invullen van onvermijdelijk afgeronde getallen in het model om het weer van de komende dagen concreet te berekenen een voorspellingshorizon van ongeveer een week opwerpen. William Boyd noemt dat in Brazzaville strand het ‘bij-gebrek-aan-een-hoefnagel-syndroom’:

Doordat men geen hoefnagel kon vinden ging de veldslag verloren. Iets kleins wordt opeens kolossaal uitvergroot. Iets rustigs raakt opeens in alle staten. Iets dat soepel verloopt wordt in een oogwenk turbulent. Hoe of waarom gebeurt zoiets? Stel, zei John, dat er kleine storingen zijn, door ons over het hoofd gezien of genegeerd; kleine irritaties die we niet van wezenlijk belang achten. Deze kleine stoornissen kunnen grote gevolgen hebben. In de wetenschap, dus ook in het leven.^[20]

Hedendaagse meteorologen dekken zich in tegen al te grote afwijkingen in het door hun voorspelde weerpatroon door voor dezelfde periode zo’n vijftig verwachtingen te berekenen, waarbij er in de beginvoorwaarden steeds kleine variaties worden aangebracht.^[21] In het geval dat de verschillende voorspellingen behoorlijk ver uiteen blijken te lopen, wordt dat er in het weerpraatje gewoon bij gezegd: ‘Voor morgen moeten we rekenen op verspreid voorkomende buien en of de zon er ook nog even bij wil komen, nou ja, dat moeten we maar afwachten.’

Een ver-uit-evenwichtsysteem, waarin kleine oorzaken grote gevolgen kunnen hebben, is aanschouwelijk te maken met een steen die precies in balans boven op de spitse top van een berg ligt. Het gewicht of de luchtverplaatsing van een landende vlinder, hoe miniem ook, kan voldoende zijn de steen uit evenwicht te brengen, zodat deze langs de helling van de berg omlaag dendert en een lawine meesleept die een dorp beneden in het dal van de aardbodem vaagt. Ook is duidelijk dat als de vlinder op een iets andere plaats landt, de steen ook een andere kant op zal vallen zonder noemenswaardige schade aan te richten. Chaostheoretici vertellen daarom graag de anekdote van de man die, gevraagd naar de reden van zijn obsessieve neiging om vlinders te vermorzelen, antwoordt dat men zich er kennelijk niet van bewust is wat voor catastrofes zo’n beest kan aanrichten. Ligt diezelfde steen eenmaal in het dal, dan is er sprake van een nieuwe evenwichtstoestand die alleen met grove middelen is te veranderen en is er weer sprake van newtoniaanse voorspelbaarheid en vergelijkbare oorzaak en gevolg.

Naast het weermodel van Lorenz zijn er nu ook vele andere voorbeelden bekend, zowel van eenvoudige als van ingewikkelde dynamische systemen, die de mogelijkheid van chaotisch gedrag vertonen, zoals turbulentie in water, wind en wolken, rookpluimen, de populatie van een diersoort gedurende een aantal generaties, ecologische en economische systemen, neuronennetwerken in de hersenen, hartfibrillatie, of de verspreiding van een epidemie. Het chaotische karakter van de economie houdt in dat de voorspellingen van de ontwikkelingen op dat gebied, met hoeveel stelligheid die doorgaans ook gebracht worden, het stadium van de natte vinger nooit te boven zullen komen, en de chaos in een ecologisch systeem is er de oorzaak van dat we er nooit helemaal maar alleen in hoge mate zeker van kunnen zijn of wijzelf de oorzaak vormen van de tot op heden gemeten verandering van het klimaat op aarde, of dat het misschien toch zo is dat er op een ongelukkig moment ergens in de wereld een vlinder is opgefladderd.

Een erg simpel en verrassend voorbeeld van een chaotisch systeem is de mechanische slinger − een bal die zo aan een touwtje is opgehangen dat hij vrijelijk in alle richtingen kan bewegen − waarvan het ophangpunt een periodieke beweging ondergaat. Geven we de slinger een zetje dan gaat deze, bij de juiste keuze van de periode van het ophangpunt, op grillige, onvoorspelbare wijze allerlei lijnen, cirkels en ellipsen doorlopen.

Sterker nog, bij herhaling van hetzelfde experiment voert de slinger totaal andere bewegingen uit, omdat het aantal mogelijke banen, afhankelijk van de precieze begintoestand, zeer groot is en er van tevoren niet valt te voorspellen welke er zal worden gevolgd. Dit mogen we toch wel ironisch noemen: de slinger die de klok moet aandrijven, eeuwenlang het schoolvoorbeeld van onverstoorbare regelmaat, blijkt naar recente inzichten makkelijk tot chao­tisch gedrag te verleiden.^[22]

Een nog interessanter geval van een eenvoudig systeem met chaotisch gedrag is het rees genoemde driedeeltjesprobleem dat Laplace voor zijn winnende essay gebruikte en waar een deel van ons zonnestelsel – de zon, de aarde en de maan – een voorbeeld van is. Uit recente computermodellen blijkt dat ons zonnestelsel op termijn chaotisch gedrag zal kunnen gaan vertonen. De vorm van de elliptische baan van Mercurius rond de zon is zeer nauwkeurig bekend, en uit duizenden computersimulaties waarin de uitgangspositie van Mercurius met minder dan een centimeter werd gevarieerd blijkt dat het lot van ons zonnestel uiterst onzeker is. Van dreigend gevaar voor moeder aarde en haar bewoners kan nog niet echt worden gesproken, want de uitkomsten van de simulaties laten ook zien dat het nog een paar miljard jaar kan duren voor Mercurius zich met catastrofale gevolgen zal gaan misdragen .^[23]

Het gebrek aan voorspellend vermogen van de betrekkelijk eenvoudige wiskundige beschrijving in deze concrete gevallen komt in de eerste plaats doordat we niet beschikken over oneindig nauwkeurige meetgegevens, maar zelfs als we die zouden hebben moeten ze ook nog noodzakelijk na een eindig aantal decimalen worden afgerond voor ze in de vergelijkingen zijn in te voeren en er met het rekenen kan worden begonnen. Tegelijk maakt de chaostheorie ons duidelijk dat we met dezelfde onzekerheden te doen hebben als het gaat om de reconstructie van het verleden, omdat we, hoe goed we de huidige situatie als uitgangstoestand ook kennen, dezelfde vergelijkingen in achterwaartse richting moeten toepassen, met dezelfde exponentieel uitvergrote onzekerheden vanuit de begintoestand.^[24] Tegenover al deze chaotische onzekerheden bestaan er ook nog steeds vele fysische processen waarvan de wiskundige vergelijkingen juist niet gevoelig zijn voor kleine veranderingen, wat ons de mogelijkheid biedt om de toekomst juist nauwkeurig te voorspellen. Daardoor is het ons recent nog gelukt om met schier eindeloze precisie een ruimtevaartuig na een ruim tien jaar durende reis over een afstand van 6,4 miljard kilometer op een passerend komeetje te laten landen.^[25]

De chaos heeft, anders dan misschien te verwachten is, een ordelijk voorkomen of faseportret. Worden de wiskundige vergelijkingen die het gedrag van een bepaald chaotisch systeem beschrijven ingevoerd in een computer, dan ontstaan na het nodige rekenwerk op het scherm de fraaiste geometrische patronen die door de ontdekker Benoït Mandelbrot fractalen zijn genoemd, omdat ze een fractale of gebroken dimensie hebben, wat men zich daarbij ook moet voorstellen: een punt is dimensieloos, een lijn heeft één dimensie, een vlak twee, een ruimtelijk lichaam drie en Einsteins tijdruimte heeft er vier, maar wat zou er een dimensie een half of tweeënhalf kunnen hebben?

Maar voor formele wiskundige operaties is dat allemaal geen probleem. Toen Mandelbrot de fascinerende structuren voor het eerst op zijn computerscherm zag verschijnen, dacht ook hij eerst, net als Lorenz, dat er sprake moest zijn van een merkwaardige computerstoring. Tegenwoordig zijn de bewegende beelden, voorzien van een passend elektronisch muziekje als computeranimaties te verkrijgen.

Dat het niet om ingewikkelde wiskundige systemen hoeft te gaan blijkt wel uit de eenvoud van de formule die tot Mandelbrots ontdekking heeft geleid: neem een variabel complex getal z – dat wil zeggen een getal met een reëel en een imaginair deel − en voer dit voor alle waarden, te beginnen bij z=0, over in z²+c, waarin c een constant complex getal is dat i (de wortel uit -1) bevat, en ziedaar een fractale structuur.

Kenmerk van fractalen is dat dezelfde structuur zich op steeds kleinere schaal herhaalt, tot in het oneindige toe, zoals dat ook het geval is met de wiskundig ingevulde witte plek of ‘godvormig gat’ in Eschers Prentententoonstelling. Hoe ver een fractaal patroon ook wordt uitvergroot, steeds keert hetzelfde beeld terug. Het zijn structuren die in de natuur overvloedig te vinden zijn, en de eenvoudigste voorbeelden zijn bomen, varens, bliksemschichten, zenuw- en bloedbanen en rivieren, die zich steeds fijner volgens hetzelfde patroon vertakken, zij het niet tot in het oneindige toe: een zijtak met twijgen is uitvergroot immers niet te onderscheiden van een tak met zijtakken of een stam met takken.

Andere voorbeelden zijn de kartelingen van kustlijnen, bergkammen en koraalriffen, de spiraalvorm van slakkenhuizen en spiraalnevels en de kristalstructuur van sneeuwvlokken. Mandelbrot schreef in The Fractal Geometry of Nature dat wetenschappers verrast en verrukt zullen zijn dat al die vormen die ze moesten betitelen als korrelig, waterachtig, ‘tussenin’, puistig, pokdalig, vertakt, zeewierachtig, vreemd, verstrengeld, kronkelend, wiebelig, sliertig, gerimpeld en dergelijke, vanaf heden op een rigoureuze en krachtige kwantitatieve wijze benaderd kunnen worden.^[26]

Eén voorbeeld verdient het wel om ter illustratie wat nader te worden uitgewerkt. De uitwendige vorm van een sneeuwkristal kan beschreven worden met wat in de wiskunde een Koch-kromme of een Koch-eiland heet’.

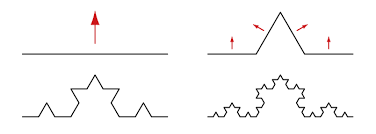
Een Koch-eiland begint met een gelijkzijdige driehoek met een zijde ter lengte van zeg 1, waarvan elke zijde in drie gelijke delen wordt verdeeld. Het middelste stuk van elke zijde dient weer als basis voor een nieuwe gelijkzijdige driehoek, maar nu met een zijde van 1/3. Elk van de oorspronkelijke zijden bestaat nu uit vier gelijke stukken die een zaagtand vormen en heeft een totale lengte van 4/3. Alle twaalf stukken worden weer in drieën gedeeld, waarna het middelste stukje, met een lengte van 1/9, weer de basis van een gelijkzijdig driehoekje is enzovoort. Na oneindige herhaling van dit proces ontstaat een gesloten gekreukelde lijn van oneindige lengte (4/3 x 4/3 x…) die toch een eindig oppervlak omsluit, omdat te bewijzen is dat het altijd kleiner blijft dan het oppervlak van de omgeschreven cirkel van de oorspronkelijke driehoek, een merkwaardig fenomeen dat de dichter Rogi Wieg inspireerde:

De sneeuwvlok is voor getallen en letters
te eigenzinnig. Dit werkstuk benadert niets,
het heeft een onmeetbare omtrek en gaat
over een niet uit te spreken bestaan.^[27]

Naast deze door het faseportret veroorzaakte verbinding tussen chaos en sneeuwkristallen, en die tussen chaos en gedachten zoals Boyd die heeft beschreven, legde Gerrit Krol met een beeld dat ook al eens door Immanuael Kant is gebruikt op zijn beurt weer verband tussen sneeuwvlokken en gedachten en maakte zo de driehoek ‘gedachten-chaos-sneeuwvlokken’ rond:

Wat is mooi? Zoals een sneeuwkristal ontstaat, zo kunnen er ook beelden in ons hoofd ontstaan − eenvoudig omdat de onderdelen ervan in elkaar passen, een andere oorzaak heeft het niet. Wat past is goed, want dat blijft zitten en wat niet past, gaat voorbij.^[28]

De grootste verrassing die de chaostheorie heeft gebracht is dat uiterst eenvoudige en overzichtelijke systemen aanleiding kunnen geven tot chaotisch, dus onvoorspelbaar gedrag. Maar hoewel de interesse gedurende de laatste jaren voor chaotische systemen aanvankelijk afkomstig is uit de meteorologie en de economie, betekent dat nog niet dat al het onvoorspelbare en ingewikkelde gedrag van het weer en de economie ook chaotisch is in de wiskundige betekenis van het woord. Lorenz’ chaotische model voor het weer is sterk vereenvoudigd in vergelijking met het werkelijke weer, en ook de modellen die in de economie worden gebruikt zijn veel simpeler dan de werkelijkheid. De Wharton Business School van de Universiteit van Pennsylvania beschikt over een van de grootste en bekendste economische modellen ter wereld, maar behaalde in een periode van tien jaar de slechtste resultaten met financiële beleggingen,^[29] terwijl er veel succesvoller werd belegd – zo gaat het verhaal – met een aandelenpakket dat werd samengesteld door een aap. Er gaapt nog een brede kloof tussen het economische of meteorologische wiskundige model en de werkelijkheid, of met andere woorden: de toepassingsmogelijkheden van de chaostheorie zijn nog zeer beperkt. Net als ten tijde van de opkomst van de kwantumtheorie en de relativiteitstheorie, toen alles opeens onzeker en relatief werd gevonden, is ook nu de verleiding groot overal chaos te ontwaren. Alom is men in de weer niet alleen eenvoudige fysische, maar ook uiterst gecompliceerde psychische, sociale, politieke en economische processen te interpreteren in termen van de chaostheorie. Maar conclusies over ingewikkelde dynamische systemen zijn op basis van de huidige stand van de chaostheorie uiterst dubieus en mogen slechts met de grootste omzichtigheid worden gehanteerd. Dat geldt met name voor beladen onderwerpen als de biologische evolutie en het chaotische gedrag van erfelijke eigenschappen bij raciale vermenging, het risico van economische nulgroei voor de stabiliteit van een samenleving, of het veronderstelde warrige functioneren van de vrouwelijke psyche, tegenwoordig allemaal gewilde studieonderwerpen. En hoewel het mogelijk is met de wiskunde van de chaos de fraaiste landschappen op het computerscherm te toveren, zijn ingewikkelde chaotische verschijnselen als klaterende beekjes en zwoele briesjes met meer succes literair of poëtisch dan fysisch of wiskundig te beschrijven, en dat geldt ook voor grillige verschijnselen als levensloop, gedachtegang of vrouwelijke nukken.

Dat neemt niet weg dat chaos als metafoor voor ingewikkelde systemen vruchtbare inzichten zou kunnen opleveren en dat er op het gebied van de chaostheorie nog vele interessante mogelijkheden te onderzoeken zijn. In ieder geval heeft de chaostheorie het wiskundig geheel gedetermineerde wereldbeeld van Newton en Laplace, in ieder geval als ware en enig mogelijke beschrijving, naar het rijk der fabelen verwezen en zal onbekendheid met bepaalde aspecten van de wereld waarin we leven een belangrijk onderdeel van ons bestaan blijven vormen. In de woorden van William Boyd, die sterk aan het scepticisme van Michel de Montaigne doen denken:

Wat nu? En toen? Al die vragen. Al die twijfels. Zo weinig zekerheden. Maar ja, ik heb een nieuwe troost en toevlucht gevonden bij de doctrine die adviseert om geen rust te zoeken in zekerheid, maar juist in een permanent opgeschort oordeel.

Hoe zou het ook anders kunnen, want niet alleen onze geest functioneert schijnbaar chaotisch, maar ook de wereld om ons heen doet zich uitermate veelvormig aan ons voor. Boyd besluit Brazzaville strand met:

Tussen de bomen verschijnen twee honden die aan het aangespoelde wier snuffelen. Mijn vlezige Syrische buurman komt in een spijkerblauwe zwembroek aanjoggen van zijn strandhuis. Hij wuift me opgewekt toe. ‘Na regen is de zee altijd frisser’, schreeuwt hij en stapt vol zelfvertrouwen de branding in. Ik zwaai terug. Een jongen houdt een oogje op drie geiten die in de palmbosjes grazen. Een krab schuifelt in zijn hol. In het dorp lacht iemand hees. De geknoopte schaduw van het volleybalnet ligt afgetekend op het strand. Ik onderzoek deze blijken van het werkelijke tegenwoordig met zorg. Het niet onderzochte leven is niet waard te worden geleefd.^[30]

Kenmerkend voor Boyds boek is dat hij de chaos als literair verschijnsel bewust aan de orde wil stellen en het er daarom willens en wetens in heeft gelegd. James Joyce daarentegen beschreef zonder die grondgedachte in zijn Ulysses de associatieve gedachtewereld van zijn protagonist Leopold Bloom in een passage die lang is maar te mooi om af te breken:

Uit schelpen, alikruiken, met een speld, van bomen, slakken zo uit de grond eten de Fransen, uit zee met aas aan een angel. Die stomme vissen hebben in duizenden jaren niets geleerd. Als men het niet wist zou het gevaarlijk zijn iets in je mond te steken. Giftige bessen. Lijsterbes. Flink rond dan is het goed. Felle kleur is men bang van. De een heeft het de ander verteld enzovoort. Probeer het eerst op de hond. Geleid door de reuk of het zien. Aanlokkelijk fruit. IJswafels. Room. Instinct. Sinaasappelbosjes bijvoorbeeld. Hebben kunstmatige besproeiing nodig. Bleibtreustrasse. Ja maar hoe zit het dan met oesters? Misschien hij wel jong vlees in bed. Nee. Juni heeft geen r geen oesters. Maar er zijn mensen die van adellijk wild houden. Hazepeper. Eerst de haas zien te vangen. Chinezen eten vijftig jaar oude eieren, blauw en weer groen. Maaltijd van dertig gangen. Elke schotel op zichzelf onschadelijk kon zich van binnen wel eens raar mengen. Idee voor een speurdersroman met vergiftiging. Was dat niet aartshertog Leopold? Nee. Ja, of was het Otto een van die Habsburgers? Wie was het ook weer die altijd de roos van zijn eigen kop opvrat?^[31]

Met de maaltijd van dertig op zich verrukkelijke gangen die zich in maag en darmen wel eens raar zouden kunnen mengen laat Joyce zien dat ook een schrijver in een chaotisch verhaal op het idee van toxische synergie kan komen. Veder valt op dat Joyce’s notities sterke overeenkomst vertonen met de gedachtegangen van een psychoot, zoals die zijn opgetekend door de ervaringsdeskundige en filosoof Wouter Kusters (zie hoofdstuk XII).

Ondanks alle chaos, werkelijk en fictief, is het probleem van de volledige gedetermineerdheid van de wereld zeker niet van de baan. Wíj zijn weliswaar niet in staat de toekomst te voorspellen omdat we de begintoestand van de wereld, als we die al zouden kennen, niet met oneindige nauwkeurigheid in de wiskundige vergelijkingen of modellen, als we die al zouden hebben, kunnen invoeren, maar dat betekent nog niet dat de wereld zélf, als die al bestaat, geen oneindig nauwkeurige toestand hééft en zijn weg zonder keuzemomenten en zonder enig spoor van twijfel tot in alle eeuwigheid kan vervolgen: het is vanuit chaostheoretisch perspectief nog steeds niet ondenkbaar dat het boek van de wereld reeds lang geleden werd geschreven en dat de tijd slechts de bladzijden voor ons omslaat. Of, zoals de zeventiende-eeuwse wiskundige Jakob Bernoulli het stelde: de toekomst móét wel bekend zijn, al was het alleen maar aan de alwetende God, hoewel zijn land- en vakgenoot Pierre Simon de Laplace een eeuw later beweerde die hypothese niet meer nodig te hebben.

Zo is het althans als we alleen de chaostheorie mogen geloven. De onzekerheid die de kwantumtheorie met zich meebrengt heeft niets met de onnauwkeurigheid van onze meetgegevens en de gevoeligheid van de berekeningen te maken en lijkt zo fundamenteel te zijn dat zelfs God, als die al bestaat, zijn greep op de loop van de dingen ermee heeft verloren, overigens zeer tegen de zin van Albert Einstein – ‘God dobbelt niet’ − maar met de volledige instemming van zijn collega Niels Bohr.

1. Met dank aan Herman Franke. ↑

2. Paul Strathern, Mendelejevs droom; De speurtocht naar de elementen, (vert. Fieke Lakmaker), Contact 2000, blz. 58. ↑

3. Asa Briggs and Daniel Snowman; Fins de Siècle, How Cen­tu­ries End, 1400-2000, Yale University Press 1996, blz. 108. ↑

4. J. Hijmans, ‘Vreemde aantrekkers, fractale structuren en de weg van voorspelbaar naar chaotisch gedrag’, uit: Chaos, Studium Generale Katholieke Universiteit Brabant 1990, blz. 30-31. ↑

5. Ilya Prigogine, Isabelle Stengers, Orde uit Chaos; De nieuwe dialoog tussen de mens en de natuur, Bert Bakker 1985, blz. 11. ↑

6. Voltaire, Filosofisch woordenboek of de rede op alfabet, (vert. en inl. J.M. Vermeer-Pardoen), Van Gennep 2001, blz. 364. ↑

7. Georg Christoph Lichtenberg, uit: Cyrille Offermans (red.), Het licht der rede; De Verlichting in brieven, essays en verhalen, Contact 2000, blz. 484. ↑

8. George Sarton, A History of Science; Ancient Science through the Golden Age of Greece, Harvard University Press 1960, blz. 416. ↑

9. Arthur Schopenhauer, De wereld als wil en voorstelling, deel 2, (vert. Hans Driessen), Wereldbibliotheek 1997, blz. 396. ↑

10. Jos Uffink, ‘Onvoorspelbaarheid in de natuurkunde’, in: Natuurkundige theo­rieën, Stu­dium Generale Universiteit Utrecht 1995. ↑

11. J. Hijmans, ‘Vreemde aantrekkers, fractale structuren en de weg van voorspelbaar naar chaotisch gedrag’, in: Chaos, Studium Generale Katholieke Universiteit Brabant 1990, blz. 31. ↑

12. Henri Poincaré, uit: Alan Sokal, Jean Bricmont, Intellectueel bedrog; Postmoder­nisme, wetenschap en anti­wetenschap, Epo De Geus 1999, blz. 126-127. ↑

13. deVolkskrant, 20-9-1991. ↑

14. William Boyd, Brazzaville strand, (vert. Rob van der Veer), Prometheus 1991, blz. 235. ↑

15. Nina Hall, (red.), The New Scientists Guide to Chaos, Penguin Books 1991, blz. 7. ↑

16. H. Tennekes, ‘Er is weer voor vijf dagen’, in: Chaos, Studium Generale Katholieke Universiteit Brabant 1990, blz. 12. ↑

17. Wiktor Eckhaus, ‘Wiskunde van de chaos’, in: Chaos, Studium Generale Katholieke Universiteit Brabant 1990, blz. 24. ↑

18. Hosea 8:7. ↑

19. Marcus du Sautoy, Wat wij niet kunnen weten; waarnemingen langs de randen van onze kennis, (vert. Dijs Translations), Nieuwezijds 2017, blz. 39-40. ↑

20. William Boyd, Brazzaville strand, (vert. Rob van der Veer), Prometheus 1991, blz. 55. ↑

21. J.D. Opsteegh, ‘Voorspelbaarheid van weer en klimaat’, in Chaos en orde, Studium Generale reeks 9903, Universiteit Utrecht 1999. ↑

22. Wiktor Eckhaus, ‘Wiskunde van de chaos’, in: Chaos, Studium Generale Katholieke Universiteit Brabant 1990, blz. 24. ↑

23. Marcus du Sautoy, Wat wij niet kunnen weten; waarnemingen langs de randen van onze kennis, (vert. Dijs Translations), Nieuwezijds 2017, blz. 54-55 ↑

24. Marcus du Sautoy, Wat wij niet kunnen weten; waarnemingen langs de randen van onze kennis, (vert. Dijs Translations), Nieuwezijds 2017, blz. 41 e.v. ↑

25. Marcus du Sautoy, Wat wij niet kunnen weten; waarnemingen langs de randen van onze kennis, (vert. Dijs Translations), Nieuwezijds 2017, blz. 62. ↑

26. Benoït Mandelbrot, uit: Richard Mankiewicz, Het verhaal van de wiskunde, Uniepers/Natuur & Techniek 2000, blz. 187.

    . ↑

27. Rogi Wieg, Sneeuwvlok, Van Oorschot 1992. ↑

28. Gerrit Krol, ‘APPI, Automatic Poetry by Pointed Information’, in: Wis- en natuurkun­de voor dichters, Studium Generale Rijksuniversiteit Utrecht 1984, blz. 50. ↑

29. Jan Bakker en Frans Janse, ‘Een veel gevraagd maar gebrekkig hulp­middel’, in: Chaos, Studium Generale Katholieke Universiteit Brabant 1990, blz. 53. ↑

30. William Boyd, Brazzaville strand, (vert. Rob van der Veer), Prometheus 1991, blz. 271. ↑

31. James Joyce, Ulysses, (vert. John Vandenbergh), De Bezige Bij 1984, blz. 203-205. ↑